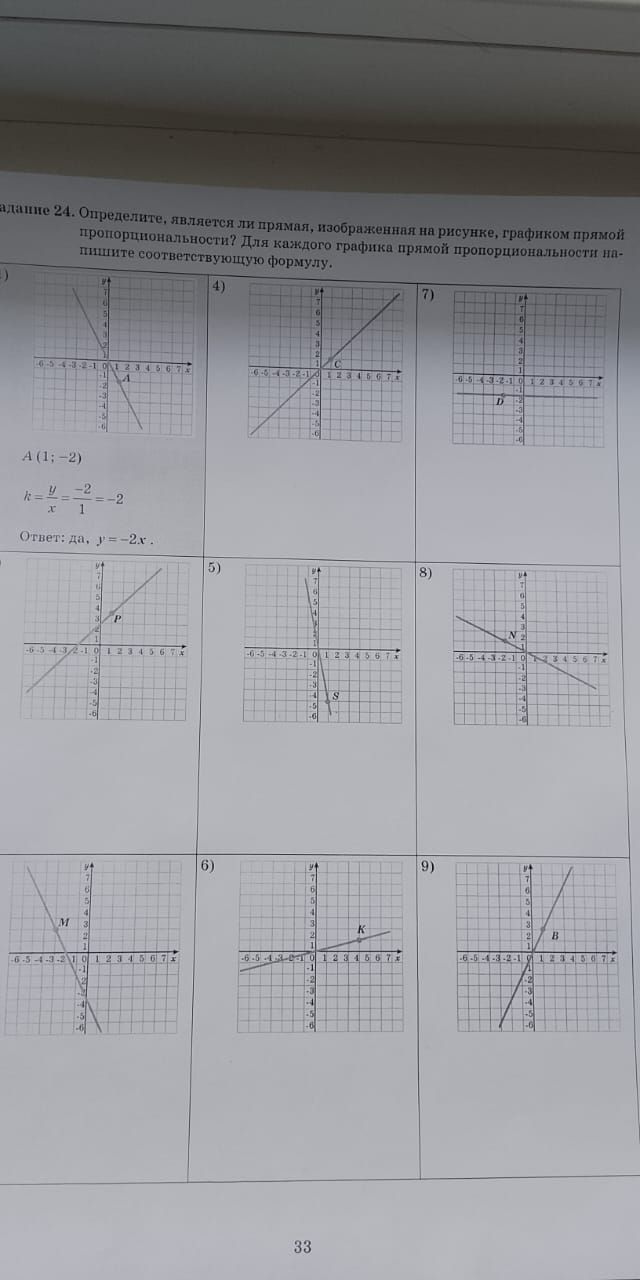
адание 24. Определите, является ли прямая, изображенная на рисунке, графиком прямой пропорциональности? Для каждого графика прямой пропорциональности на- пишите соответствующую формулу. ) 65-4-3-2-1012 A (1;-2) 4) -6-6-4-3-2-1 123466 7) Ответ: да, у=-2x. P 5) 8) +++ -6-5-4-32-10 12345674 M 6) -6-5-4-3-2-1 01234567 S K 9) 6-5-4-3-2-10234567A B + + + -6-5-43-010 12345678 -6-5-4-3-2-19 12345

Определим, является ли прямая, изображенная на рисунке, графиком прямой пропорциональности, и для каждого графика прямой пропорциональности напишем соответствующую формулу.

1. На рисунке 1 изображена прямая, проходящая через точку A(1;-2). Прямая пропорциональность имеет вид y=kx, где k - коэффициент пропорциональности. Подставим координаты точки А в уравнение: $$ k = \frac{y}{x} = \frac{-2}{1} = -2 $$ Да, это прямая пропорциональность. Ответ: да, $$y = -2x$$.
2. На рисунке 4 изображена прямая, проходящая через начало координат. Выберем точку С(1;2) на прямой. $$k = \frac{y}{x} = \frac{2}{1} = 2$$ Ответ: да, $$y = 2x$$.
3. На рисунке 7 изображена прямая, параллельная оси x и проходящая через точку D(0;-3). Это не прямая пропорциональность, так как она не проходит через начало координат. Ответ: нет.
4. На рисунке 2 изображена прямая, проходящая через точку P(1;4). $$k = \frac{y}{x} = \frac{4}{1} = 4$$ Ответ: да, $$y = 4x$$.
5. На рисунке 5 изображена прямая, проходящая через точку S(1;-5). $$k = \frac{y}{x} = \frac{-5}{1} = -5$$ Ответ: да, $$y = -5x$$.
6. На рисунке 8 изображена прямая, проходящая через точку N(2;1). $$k = \frac{y}{x} = \frac{1}{2} = 0,5$$ Ответ: да, $$y = 0,5x$$.
7. На рисунке 3 изображена прямая, проходящая через точку M(-1;3). $$k = \frac{y}{x} = \frac{3}{-1} = -3$$ Ответ: да, $$y = -3x$$.
8. На рисунке 6 изображена прямая, проходящая через точку K(4;1). $$k = \frac{y}{x} = \frac{1}{4} = 0,25$$ Ответ: да, $$y = 0,25x$$.
9. На рисунке 9 изображена прямая, проходящая через точку B(1;5). $$k = \frac{y}{x} = \frac{5}{1} = 5$$ Ответ: да, $$y = 5x$$.