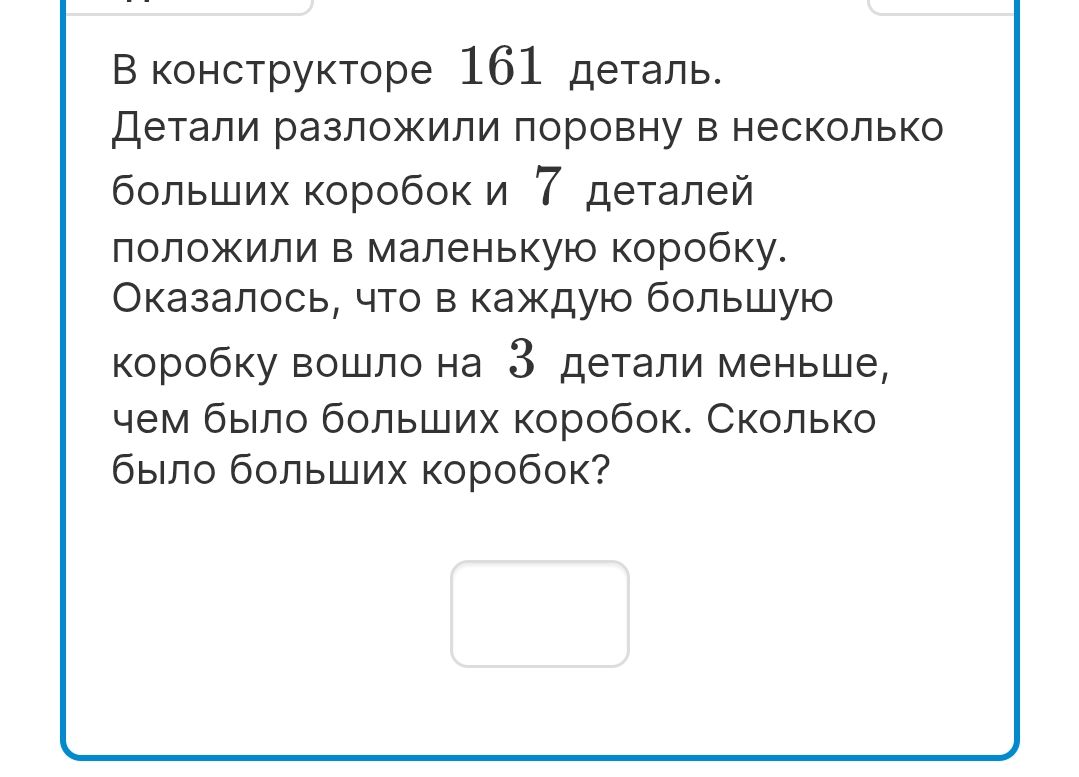
В конструкторе 161 деталь. Детали разложили поровну в несколько больших коробок и 7 деталей положили в маленькую коробку. Оказалось, что в каждую большую коробку вошло на 3 детали меньше, чем было больших коробок. Сколько было больших коробок?

Решение:

Пусть x - количество больших коробок.

Тогда (х - 3) - количество деталей в каждой большой коробке.

Всего в большие коробки положили х(х - 3) деталей.

В маленькую коробку положили 7 деталей.

Всего деталей 161.

Составим уравнение:

$$x(x-3) + 7 = 161$$

$$x^2 - 3x + 7 = 161$$

$$x^2 - 3x - 154 = 0$$

Решим квадратное уравнение:

$$D = (-3)^2 - 4 \cdot 1 \cdot (-154) = 9 + 616 = 625$$

$$x_1 = \frac{-(-3) + \sqrt{625}}{2 \cdot 1} = \frac{3 + 25}{2} = \frac{28}{2} = 14$$

$$x_2 = \frac{-(-3) - \sqrt{625}}{2 \cdot 1} = \frac{3 - 25}{2} = \frac{-22}{2} = -11$$

Так как количество коробок не может быть отрицательным, то подходит только корень 14.

Ответ: 14