ГДЗ по геометрии 7 класс Атанасян ФГОС Вопросы для повторения к главе XV

\[\boxed{\mathbf{Вопросы\ для\ повторения\ к\ главе\ }\mathbf{\text{XV}}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]

\[\boxed{\mathbf{1.}}\]

\[Многоугольник\ \ F_{1}\text{\ \ }\]

\[называется\ \ подобным\ \ \]

\[одноимённому\ \ \]

\[многоугольнику\ \ F,\ если\ \ углы\ \]

\[многоугольника\ \ F_{1}\ \]

\[соответственно\ \ равны\ \ углам\ \]

\[многоугольника\ \ F,\ а\ \ их\ \ \]

\[сходственные\ \ стороны\ \]

\[пропорциональны.\]

\[\boxed{\mathbf{2.}}\]

\[Число\ \ k,\ равное\ \ отношению\ \ \]

\[сходственных\ сторон\ \ \]

\[многоугольников\ F_{1}\ \ и\ \ F,\]

\[\ называется\ \ коэффициентом\ \ \]

\[подобия\ многоугольников.\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{если\ \ два\ \ многоугольника\ \ }\]

\[\mathbf{подобны\ \ и\ \ коэффициент\ \ }\]

\[\mathbf{подобия\ \ равен\ единице,\ то\ \ }\]

\[\mathbf{такие\ \ многоугольники\ \ равны.}\]

\[\boxed{\mathbf{4.}}\]

\[Теорема:\]

\[отношение\ \ периметров\ \ двух\ \ \]

\[подобных\ \ многоугольников\]

\[равно\ коэффициенту\ \ подобия\ \]

\[многоугольников.\]

\[Доказательство.\]

\[Пусть\ A_{1}A_{2}\ldots A_{n}\ подобен\]

\[\ B_{1}B_{2}\ldots B_{n}\ с\ коэффициентом\ \text{k.}\]

\[Тогда:\]

\[A_{1}A_{2} = k \cdot B_{1}B_{2};\]

\[A_{2}A_{3} = k \cdot B_{2}B_{3};\]

\[A_{n}A_{1} = k \cdot B_{n}B_{1}.\]

\[Найдем\ отношение\ \]

\[периметров\ данных\ \]

\[многоугольников:\]

\[\frac{A_{1}A_{2} + A_{2}A_{3} + \ldots + A_{n}A_{1}}{B_{1}B_{2} + B_{2}B_{3} + \ldots + B_{n}B_{1}} =\]

\[= \frac{k\left( B_{1}B_{2} + B_{2}B_{3} + \ldots + B_{n}B_{1} \right)}{B_{1}B_{2} + B_{2}B_{3} + \ldots + B_{n}B_{1}} =\]

\[= k.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{5.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{отношение\ площадей\ двух\ }\]

\[\mathbf{подобных\ многоугольников\ \ }\]

\[\mathbf{равно\ квадрату\ \ коэффициента\ \ }\]

\[\mathbf{подобия.}\]

\[Доказательство.\]

\[Поскольку\ \ ход\ \ рассуждений\ \ \]

\[не\ \ зависит\ \ \ от\ \ числа\ \ сторон\ \]

\[этих\ многоугольников,\ \]

\[рассмотрим\ \ для\ \ \]

\[определённости\ \ случай,\]

\[\ когда\ \ \]

\[n\ = \ 5.\]

\[Пусть\ A_{1}A_{2}A_{3}A_{4}A_{5}\ подобен\ \]

\[B_{1}B_{2}B_{3}B_{4}B_{5}\ с\ коэффициентом\]

\[\ \text{k.}\]

\[По\ определению\ подобных\ \]

\[многоугольников:\]

\[A_{1}A_{2} = k \cdot B_{1}B_{2};\]

\[A_{2}A_{3} = k \cdot B_{2}B_{3};\]

\[A_{3}A_{4} = k \cdot B_{3}B_{4};\]

\[A_{4}A_{5} = k \cdot B_{4}B_{5};\]

\[A_{5}A_{1} = k \cdot B_{5}B_{1}.\]

\[\mathbf{Разобьем\ многоугольники\ }\]

\[\mathbf{на\ треугольники:}\]

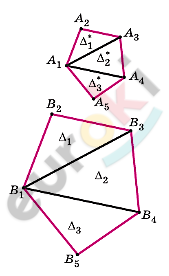
\[⊿_{1}^{*}\sim ⊿_{1};\ \ ⊿_{2}^{*}\sim ⊿_{2};\ \ ⊿_{3}^{*}\sim ⊿_{3} -\]

\[по\ второму\ признаку\ подобия\ \]

\[треугольников.\]

\[\mathbf{Согласно\ теореме\ о\ площадях\ }\]

\[\mathbf{подобных\ треугольников:}\]

\[S_{⊿_{1}^{*}} = k^{2}S_{⊿_{1}};\ \ S_{⊿_{2}^{*}} = k^{2}S_{⊿_{2}};\ \]

\[\ S_{⊿_{3}^{*}} = k^{2}S_{⊿_{3}}.\]

\[Складываем\ три\ равенства:\]

\[S_{⊿_{1}^{*}} + S_{⊿_{2}^{*}} + S_{⊿_{3}^{*}} =\]

\[= k^{2}S_{⊿_{1}} + k^{2}S_{⊿_{2}} + k^{2}S_{⊿_{3}}.\]

\[Учитывая\ известное\ свойство\ \]

\[площадей\ (п.\ 54):\]

\[S_{A_{1}A_{2}A_{3}A_{4}A_{5}} = k^{2}S_{B_{1}B_{2}B_{3}B_{4}B_{5}}\]

\[\frac{S_{A_{1}A_{2}A_{3}A_{4}A_{5}}}{S_{B_{1}B_{2}B_{3}B_{4}B_{5}}} = k^{2}.\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{6.}}\]

\[Пусть\ F - данная\ фигура\ и\ \]

\[O - фиксированная\ точка;\]

\[Проведем\ через\ \]

\[произвольную\ точку\ X\ \]

\[фигуры\ \text{F\ }луч\ \text{OX\ }и\ отложим\]

\[на\ нем\ отрезок\ OX^{'},\]

\[\ равный\ k \bullet OX,\ где\ k -\]

\[положительное\ число.\]

\[1)\ Преобразование\ фигуры\ F,\ \]

\[при\ котором\ каждая\ ее\ точка\ \]

\[\text{X\ }переходит\ в\ точку\ X^{'}\ \]

\[указанным\ способом,\ \]

\[называется\ гомотетией\ \]

\[относительно\ центра\ \text{O.}\]

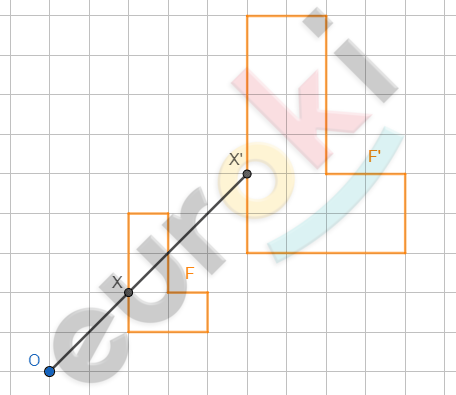
\[Фгуры\ \text{F\ }и\ F^{'}\ гомотетичны\ \]

\[относительно\ центра\ \text{O.}\]

\[\boxed{\mathbf{7.}}\]

\[Пусть\ F - данная\ фигура\ и\ \]

\[O - фиксированная\ точка;\]

\[Проведем\ через\ произвольную\ \]

\[точку\ X\ фигуры\ \text{F\ }луч\ \text{OX\ }\]

\[и\ отложим\ на\ нем\ отрезок\ OX^{'},\ \]

\[равный\ k \bullet OX,\ где\ k -\]

\[положительное\ число.\]

\[1)\ Точка\ O - является\ \]

\[центром\ гомотетии.\]

\[2)\ Число\ \text{k\ }называется\ \]

\[коэффициентом\ гомотетии.\]

\[\boxed{\mathbf{8.}}\]

\[\textbf{а)}\ Если\ \ коэффициент\ \ \]

\[гомотетии\ \ равен\ \ единице,\ то\ \ \]

\[все\ \ точки\ \ плоскости,\ а\ \ значит,\]

\[\ и\ \ любой\ фигуры\ \ F\ \ остаются\ \ \]

\[неподвижными,\ т.\ \ е.\ \ фигура\ \]

\[переходит\ \ сама\ \ в\ \ себя.\ \ \]

\[\textbf{б)}\ Если\ \ k = \ –1,\ то\ \ каждая\ \]

\[точка\ \ фигуры\ \ F\ \ переходит\ \ в\ \ \]

\[симметричную\ \ ей\ \ точку\ \ \]

\[относительно\ \ центра\ \ O,\ \]

\[поэтому\ \ фигура\ \ F_{1}\ получается\ \ \]

\[центральной\ \ симметрией\ \ \]

\[из\ \ фигуры\ \ F.\ \]

\[\boxed{\mathbf{9.}}\]

\[Три\ основных\ свойства\ \]

\[гомотетии.\]

\[1)\ При\ \ гомотетии\ \ \]

\[с\ \ коэффициентом,\ отличным\ \]

\[от\ \ единицы,\ прямая,\ \ \]

\[проходящая\ \ через\ \ центр\ \]

\[гомотетии,\ переходит\ \ в\ \ себя,\ \]

\[а\ \ прямая,\ не\ проходящая\ \ \]

\[через\ \ центр\ \ гомотетии,\ —\ \ \]

\[в\ \ параллельную\ \ ей\ \ прямую.\]

\[2)\ Если\ \ при\ \ гомотетии\ \ \]

\[с\ \ коэффициентом\ \ k\ \ концы\ \ \]

\[отрезка\ \ AB\ переходят\ \ \]

\[в\ \ точки\ \ A_{1}\ \ и\ \ B_{1},\ то\ отрезок\ \]

\[\text{AB\ }переходит\ в\ отрезок\ A_{1}B_{1},\]

\[причем\ A_{1}B_{1} = k\left| \text{AB} \right|.\]

\[3)\ При\ \ гомотетии\ \ \]

\[с\ \ коэффициентом\ \ k\ \ \]

\[окружность\ \ с\ \ центром\ \ C\ \ и\ \ \]

\[радиусом\ \ r\ \ переходит\ \ \]

\[в\ окружность\ \ с\ \ центром\ \ C_{1}\text{\ \ }\]

\[и\ \ радиусом\ \ |k|r,\ \ \]

\[где\ C_{1}\ —\ \ точка,\ в\ \ которую\ \ \]

\[переходит\ \ точка\ \ C.\ \]

\[\boxed{\mathbf{10.}}\]

\[\mathbf{Верно:третье\ свойство\ }\]

\[\mathbf{гомотетии.}\]

\[\boxed{\mathbf{11.}}\]

\[\mathbf{Верно:следует\ из\ первого\ }\]

\[\mathbf{и\ второго\ свойств\ гомотетии.}\]

\[\boxed{\mathbf{12.}}\]

\[Теорема:\]

\[при\ гомотетии\ \]

\[с\ коэффициентом\ k\ \]

\[многоугольник\ переходит\ \]

\[в\ подобный\ ему\ \]

\[многоугольник,\ причём\ \]

\[коэффициент\ \ подобия\ \]

\[многоугольников\ \ \]

\[равен\ \ |k|.\]

\[Доказательство.\]

\[Пусть\ A_{1}A_{2}\ldots A_{n} -\]

\[произвольный\ \]

\[многоугольник.\ Из\ второго\ \]

\[свойства\ гомотетии\ следует,\ \]

\[что\ при\ гомотетии\ \]

\[с\ коэффициентом\ k\ этот\]

\[многоугольник\ переходит\ \]

\[в\ многоугольник\ B_{1}B_{2}\ldots B_{n}.\]

\[Причем:\]

\[B_{1}B_{2} = |k|A_{1}A_{2};\]

\[B_{2}B_{3} = |k|A_{2}A_{3};\]

\[B_{n}B_{1} = |k|A_{n}A_{1}.\]

\[При\ гомотетии\ угол\ \]

\[переходит\ в\ равный\ ему\ угол:\]

\[\angle B_{1} = A_{1};\ \ \ \angle B_{2} = \angle A_{2};\ \]

\[\ \angle B_{n} = \angle A_{n}.\]

\[Из\ полученных\ равенств\ \]

\[заключаем,\ что\ \]

\[многоугольники\ подобны\ с\ \]

\[коэффициентом\ k.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{13.}}\]

\[\mathbf{Две\ фигуры\ называются\ }\]

\[\mathbf{подобными,\ если\ они\ }\]

\[\mathbf{переводятся\ друг\ в\ друга}\]

\[\mathbf{преобразованием\ подобия.}\]

\[\mathbf{Из\ свойств\ подобия\ следует:}\]

\[\mathbf{у\ подобных\ фигур\ }\]

\[\mathbf{соответствующие\ углы\ равны,\ }\]

\[\mathbf{а\ соответствующие\ отрезки\ }\]

\[\mathbf{пропорциональны.}\]

\[\boxed{\mathbf{14.}}\]

\[Коэффициентом\ подобия\ \]

\[называют\ число\ k,\ равное\ \]

\[отношению\ с\]

\[сходственных\ сторон\ \]

\[подобных\ треугольников.\]

\[Коэффициент\ подобия\ \]

\[не\ может\ быть\ \]

\[отрицательным\ числом.\]

\[\boxed{\mathbf{15.}}\]

\[Свойства\ подобия\ фигур.\]

\[1)\ если\ фигура\ F_{1}\ подобна\ \]

\[фигуре\ \text{F\ }с\ коэффициентом\ k,\ \]

\[то\ фигура\ F\ подобна\ фигуре\ F_{1}\ \]

\[с\ коэффициентом\ \frac{1}{k}.\]

\[2)\ если\ фигура\ F_{2}\ подобна\ \]

\[фигуре\ F_{1}\ с\ коэффицентом\ n,\ \]

\[а\ фигура\ F_{1}\ подобна\ фигуре\ F\ \]

\[с\ коэффициентом\ k,\ то\ фигура\]

\[\ F_{2}\ подобна\ фигуре\ F\]

\[с\ коэффициентом\ \text{nk.}\]

\[\boxed{\mathbf{16.}}\]

\[O - центр\ гомотетии;\]

\[A;A_{1} - соответственные\]

\[точки.\]

\[\textbf{а)}\ F - точка:\]

\[Пусть\ P - произвольная\ точка\ \]

\[плоскости,\ не\ лежащая\ \]

\[на\ прямой\ \text{OA.}\]

\[Проведем\ через\ точку\ A_{1}\ \]

\[прямую \parallel \text{AP.}\]

\[Точка\ P_{1} - пересечение\ ее\ \]

\[с\ прямой\ \text{OP.}\]

\[Если\ точка\ P\ лежит\ на\ прямой\ \]

\[\text{OA},\ то\ сначала\ выберем\ \]

\[произвольную\ точку\ \text{Q\ }вне\]

\[прямой\ \text{OA\ }и\ построим\ \]

\[гомотетичную\ ей\ точку\ Q_{1}.\]

\[После\ этого,\ используя\ пару\ \]

\[гомотетичных\ точек\ Q\ и\ Q_{1}\ \]

\[строим\ искомую\ точку\ P_{1},\]

\[описанным\ выше\ способом.\]

\[\textbf{б)}\ F - многоугольник:\]

\[Построение\ многоугольника\ \]

\[сводится\ к\ построению\ \]

\[отрезка.\]

\[Отложим\ на\ произвольном\ \]

\[луче,\ исходящем\ из\ точки\ O,\ \]

\[отрезки\ OA = n;\ \ OA_{1} = m.\ \ \]

\[k = \frac{m}{n}.\]

\[Построим\ затем\ точки\ P_{1}\ и\ Q_{1},\ \]

\[гомотетичные\ точкам\ P\ и\ \text{Q.\ }\]

\[Отрезок\ P_{1}Q_{1} - искомый.\]

\[Если\ точки\ \text{P\ }и\ \text{Q\ }не\ лежат\ \]

\[на\ одной\ прямой\ с\ точкой\ O,\ \]

\[то\ можно\ сначала\ ранее\ \]

\[указанным\ способом\ \]

\[построить\ точку\ P_{1},\]

\[гомотетичную\ точке\ P,\ а\ затем\ \]

\[провести\ через\ нее\ прямую\]

\[\parallel PQ.\]

\[Q_{1} - точка\ ее\ пересечения\ \]

\[с\ прямой\ \text{OQ.}\]

\[Отрезок\ P_{1}Q_{1} - искомый.\]

\[Пример:\]

\[построение\ трапеции,\ \]

\[гомотетичной\ данной.\]

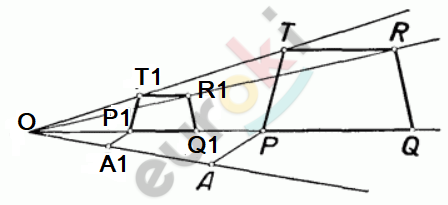
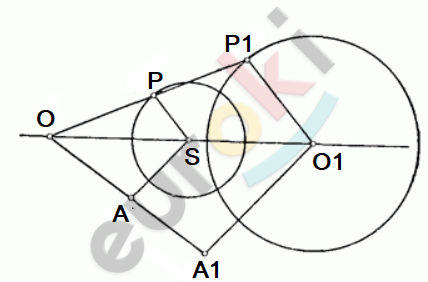
\[\textbf{в)}\ F - окружность:\]

\[Для\ построения\ гомотетичной\ \]

\[окружности\ достаточно\ \]

\[построить\ точки,\ \]

\[соответственно\ гомотетичные\ \]

\[центру\ данной\ окружности\ и\ \]

\[точки\ на\ ней.\]

\[OA = n;\ \ OA_{1} = m;\ \ k = \frac{m}{n};\]

\[A_{1}O_{1} \parallel AS;\]

\[O_{1}P_{1} \parallel SP;\]

\[P - произвольная\ точка\ \]

\[на\ окружности.\]

\[\boxed{\mathbf{17.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{если\ \ две\ \ хорды\ \ окружности\ \ }\]

\[\mathbf{пересекаются,\ то\ }\]

\[\mathbf{произведение\ \ отрезков\ \ одной\ \ }\]

\[\mathbf{хорды\ \ равно\ \ произведению\ \ }\]

\[\mathbf{отрезков\ \ другой\ \ хорды.}\]

\[\mathbf{Доказательство.}\]

\[Пусть\ хорды\ окружности\ \text{AB\ }\]

\[и\ \text{CD\ }пересекаются\ в\ точке\ \text{M.}\]

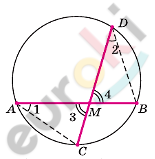
\[⊿AMC\ подобен\ ⊿DBM -\]

\[по\ первому\ признаку:\]

\[\angle 1 = \angle 2 - вписанные\ \]

\[в\ окружность\ и\ опираются\ \]

\[на\ одну\ и\ ту\ же\ дугу;\]

\[\angle 3 = \angle 4 - вертикальные.\]

\[Отсюда:\]

\[\frac{\text{MA}}{\text{MD}} = \frac{\text{MC}}{\text{MB}}\]

\[MA \cdot MB = MC \cdot MD.\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{18.}}\]

\[Теорема:\]

\[если\ через\ \ внешнюю\ точку\ \ \]

\[к\ окружности\ \ проведены\ \ \]

\[касательная\ \ и\ \ секущая,\ то\ \ \]

\[квадрат\ \ отрезка\ \ касательной\ \ \]

\[равен\ \ произведению\ \ \]

\[отрезков\ секущей.\]

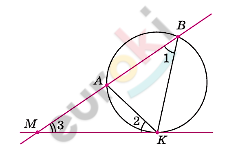
\[Доказательство.\ \]

\[Рассмотрим\ \ треугольники\ \]

\[\ MKA\ \ и\ \ MBK\ и\ \ докажем,\ что\ \ \]

\[они\ \ подобны.\ \]

\(\ \)

\[Действительно,\ углы\ \ 1\ \ и\ \ 2\ \ \]

\[равны,\ так\ \ как\ \ каждый\ \ \]

\[из\ них\ \ измеряется\ половиной\ \ \]

\[дуги\ \ АK:\]

\[\angle 1\ \ —\ \ вписанный\ \ \]

\[в\ \ окружность\ \]

\[\ и\ \ опирающийся\ \ на\ \ дугу\ \ АK;\ \ \]

\[\angle 2\ \ —\ \ угол\ \ между\ \ \]

\[касательной\ \ к\ \ окружности\ \ \]

\[и\ хордой.\ \ \]

\[\angle 3\ \ —\ \ общий\ \ угол\ \ этих\ \ \]

\[треугольников.\ \]

\[⊿MKA\ подобен\ ⊿MBK -\]

\[по\ первому\ признаку.\]

\[Отсюда:\]

\[\frac{\text{MK}}{\text{MB}} = \frac{\text{MA}}{\text{MK}}\]

\[MK^{2} = MA \cdot MB.\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{19.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{если\ \ через\ \ точку,\ лежащую\ \ }\]

\[\mathbf{вне\ \ окружности,\ проведены\ \ }\]

\[\mathbf{две\ \ секущие,\ то\ \ произведение\ \ }\]

\[\mathbf{отрезков\ \ одной\ \ секущей\ \ }\]

\[\mathbf{равно\ \ произведению\ \ }\]

\[\mathbf{отрезков\ \ другой\ \ секущей.}\]

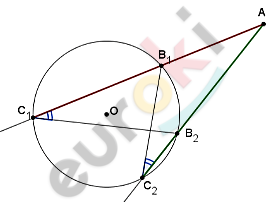
\[Доказательство.\]

\[⊿AC_{1}B_{2}\ подобен\ ⊿AC_{2}B_{1} -\]

\[по\ двум\ углам:\]

\[\angle A - общий;\]

\[\angle C_{1} = \angle C_{2} - как\ вписанные\ \]

\[углы,\ опирающиеся\ на\ дугу\ \]

\[B_{1}B_{2}.\]

\[Отсюда:\]

\[\frac{AC_{1}}{AC_{2}} = \frac{AB_{2}}{AB_{1}}\]

\[По\ свойству\ пропорции:\]

\[AC_{1} \cdot AB_{1} = AC_{2} \cdot AB_{2}.\]

\[\boxed{\mathbf{20.}}\]

\[\mathbf{Дано:}\]

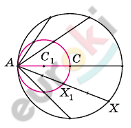
\[\mathbf{Доказательство.}\]

\[При\ \ гомотетии\ \ с\ \ центром\ \ \]

\[в\ \ точке\ \ A\ \ и\ \ коэффициентом\ \]

\[\ k = \frac{1}{2}\text{\ \ }\]

\[любая\ \ точка\ \ X\ \ окружности\ \ \]

\[с\ центром\ \ C\ \ и\ \ радиусом\ \ r\ \ \]

\[перейдёт\ в\ точку\ \ X_{1}\ \ —\ \]

\[середину\ \ хорды\ \ AX.\ \ \]

\[По\ \ свойству\ \ 30\ \ п.\ \ 134\ \ \]

\[при\ указанной\ \ гомотетии\ \ \]

\[окружность\ с\ центром\ \ C\ \ \ \ \]

\[и\ \ радиусом\ \ r\ \ переходит\ \ \]

\[в\ \ окружность\ \ с\ \ центром\ \ C_{1}\ в\ \ \]

\[середине\ \ отрезка\ \ AC\ \ \]

\[и\ \ радиусом\ \ r_{1} = \frac{1}{2}\text{r.\ \ }\]

\[Эта\ окружность\ \ и\ \ является\ \ \]

\[искомым\ \ множеством\ \ точек.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{21.}}\]

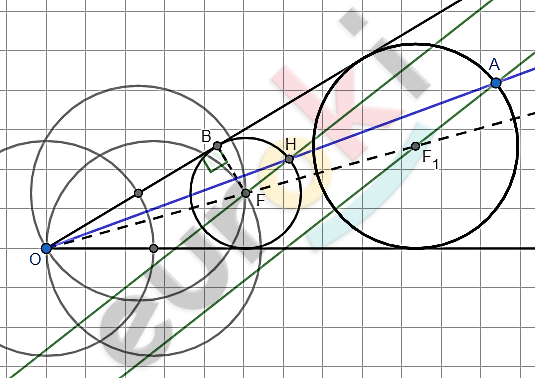
\[Построение.\]

\[1)\ Пусть\ даны\ угол\ \text{O\ }\]

\[и\ точка\ \text{A.}\]

\[2)\ Построим\ биссектрису\ OF\ \]

\[угла\ \text{O.}\]

\[3)\ Из\ точки\ F\ опустим\ \]

\[перендикуляр\ \text{FB\ }на\ одну\ \]

\[из\ сторон\ угла\ \text{O.}\]

\[4)\ Проведем\ окружность\ \]

\[с\ центром\ в\ точке\ \text{F\ }\]

\[и\ радиусом\ равным\ FB_{1},эта\ \]

\[окружность\ касается\ обеих\ \]

\[сторон\ угла,\ так\ как\ точка\ F\ \]

\[лежит\ на\ биссектрисе\ OF,\ \]

\[которая\ равноудалена\ от\ его\ \]

\[сторон.\]

\[5)\ Проведем\ луч\ \text{OA\ }и\ отметим\ \]

\[точку\ \text{H\ }на\ одном\ из\ \]

\[пересечений\ этого\ луча\ \]

\[и\ окружности.\]

\[6)\ Через\ точку\ A\ проведем\ \]

\[прямую,\ параллельную\ прямой\ \]

\[\text{HF\ }и\ отметим\ точку\ F_{1}\ \]

\[на\ пересечении\ этой\ прямой\ \]

\[и\ биссектрисы\ \text{OF.}\]

\[7)\ Проведем\ окружность\ \]

\[с\ центром\ в\ точке\ F_{1}\ \]

\[и\ радиусом\ равным\ F_{1}A,\ эта\ \]

\[окружность\ является\ искомой.\ \]