ГДЗ по геометрии 8 класс Атанасян ФГОС Вопросы для повторения к главе XII
Вопросы для повторения к главе XII
\[\boxed{\mathbf{Вопросы\ для\ повторения\ к\ главе\ }\mathbf{\text{XII}}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]
\[\boxed{\mathbf{1.}}\]
\[\boxed{\mathbf{2.}}\]

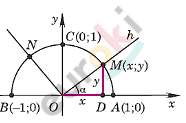
\[Для\ любого\ угла\ \alpha\ \]
\[из\ промежутка\ 0{^\circ} \leq \alpha \leq 180{^\circ}\ \]
\[синусом\ угла\ \alpha\ называется\ \]
\[ордината\ \text{y\ }точки\ M,\ а\ \]
\[косинусом\ угла\ \alpha - абсцисса\ \text{x\ }\]
\[точки\ M.\]
\[\boxed{\mathbf{3.}}\]
\[Тангенсом\ угла\ \alpha\ (\alpha \neq 90{^\circ})\ \]
\[называется\ отношение\ \frac{\sin\alpha}{\cos\alpha}:\]
\[tg\ \alpha = \frac{\sin\alpha}{\cos\alpha}.\]
\[При\ \alpha = 90{^\circ}\ \ tg\ \alpha\ не\ определен,\ \]
\[поскольку\cos{90{^\circ}} = 0;\]
\[знаменатель\ обращается\ в\ 0,\ а\ \]
\[на\ ноль\ делить\ нельзя.\]
\[\boxed{\mathbf{4.}}\]
\[Котангенсом\ угла\text{\ α}\]
\[\ (0{^\circ} \leq \alpha \leq 180{^\circ})называется\ \]
\[отношение\ \frac{\cos\alpha}{\sin\alpha}:\ \]
\[ctg\ \alpha = \frac{\cos\alpha}{\sin\alpha}.\]
\[При\ \alpha = 0{^\circ};\ \ a = 180{^\circ}\ \ ctg\ \alpha\ \]
\[не\ определен,\ потому\ что\ \]
\[знаменатель\ обращается\ \]
\[в\ ноль.\]
\[\boxed{\mathbf{5.}}\]
\[Основное\ тригонометрическое\ \]
\[тождество:\]
\[\text{si}n^{2}\alpha + cos^{2}\alpha = 1.\]
\[Доказательство.\]

\[Пусть\ \alpha - угол\ между\ лучом\ \text{h\ }\]
\[и\ положительной\ полуосью\ \]
\[абсцисс.\]
\[Данная\ полуокружность\ \]
\[является\ дугой\ окружности,\ \]
\[которая\ имеет\ уравнение\ \]
\[x^{2} + y^{2} = 1\ (1).\]
\[\sin\alpha = y;\ \cos\alpha = x:\]
\[Подставим\ в\ уравнение\ (1)\ \]
\[и\ получим:\]
\[\text{si}n^{2}\alpha + cos^{2}\alpha = 1;\]
\[которое\ выполняется\ \]
\[для\ любого\ \alpha\ из\ промежутка\ \]
\[0{^\circ} \leq \alpha \leq 180{^\circ}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{6.}}\]
\[Формулы\ приведения.\]
\[При\ 0{^\circ} \leq \alpha \leq 90º.\]
\[\sin{(90{^\circ} - \alpha}) = \cos\alpha;\]
\[\cos(90{^\circ} - \alpha) = \sin\alpha.\]
\[При\ 0{^\circ} \leq \alpha \leq 180{^\circ}:\]
\[\sin(180{^\circ} - \alpha) = \sin\alpha;\]
\[\cos(180{^\circ} - \alpha) = - \cos\alpha.\]
\[\boxed{\mathbf{7.}}\]
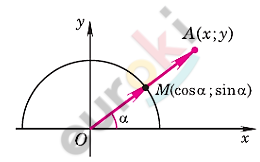
\[\mathbf{Выведем\ формулы.}\]
\[Пусть\ \ задана\ \ система\ \ \]
\[координат\ \ Oxy\ \ и\ \ дана\ \]
\[произвольная\ точка\ \text{A\ }(x;y)\]
\[с\ неотрицательной\ \]
\[ординатой\ y.\ \ \]
\[Выразим\ \ координаты\ \ точки\ \]
\[A\ \ через\ \ длину\ \ отрезка\ \ OA\ \ и\ \ \]
\[угол\ \ \alpha\ \ между\ \ лучом\ \ OA\ \ и\ \ \]
\[положительной\ \ полуосью\ Ox.\ \ \]
\[Для\ \ этого\ \ обозначим\ \ буквой\ \ \]
\[M\ \ точку\ пересечения\ \ луча\ \ \]
\[\text{OA}\ \ с\ единичной\ \ \]
\[полуокружностью.\ \ \]
\[По\ \ формулам:\]
\[координаты\ \ точки\ \ M\ \ \]
\[соответственно\ \ равны\ \ c\]
\[os\ \alpha,\ sin\ \alpha.\ \]
\[Вектор\ \overrightarrow{\text{OM}}\ имеет\ те\ же\ \]
\[координаты,\ что\ и\ точка\ M:\]
\[\overrightarrow{\text{OM}}\left\{ \cos\alpha;\sin\alpha \right\}.\]
\[Вектор\ \overrightarrow{\text{OA}}\ имеет\ те\ же\ \]
\[координаты,\ что\ и\ точка\ A:\]
\[\overrightarrow{\text{OA}}\left\{ x;y \right\}.\]
\[\overrightarrow{\text{OA}} = OA \cdot \overrightarrow{\text{OM}}:\]
\[x = OA \cdot \cos\alpha;\]
\[y = OA \cdot \sin\alpha.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{8.}}\]
\[Теорема:\]
\[площадь\ треугольника\ равна\ \]
\[половине\ произведения\ двух\ \]
\[его\ сторон\ на\ синус\ угла\ \]
\[между\ ними.\]
\[Дано:\]
\[⊿ABC;\]
\[BC = a;\]
\[CA = b;\]
\[S - площадь.\]
\[Доказать:\]
\[S = \frac{1}{2}ab \cdot \sin C.\]
\[Доказательство.\]
\[Введём\ \ систему\ \ координат\ \ \]
\[с\ \ началом\ \ в\ \ точке\ \ C\ \ так,\ \]
\[чтобы\ \ точка\ B\ лежала\ \ \]
\[на\ \ положительной\ \ полуоси\ \]
\[\ Cx,\ а\ \ точка\ \ A\ \ имела\ \ \]
\[положительную\ \ ординату.\ \ \]
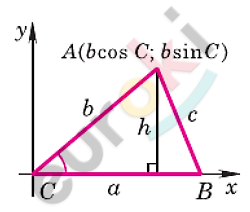
\[Площадь\ \ данного\ \]
\[треугольника\ \ можно\ \ \]
\[вычислить\ \ по\ \ формуле:\]
\[S = \frac{1}{2}ah;\ \ h - высота\ \]
\[треугольника.\]
\[Но\ \text{h\ }равна\ ординате\ точки\ A:\]
\[h = b \cdot \sin C.\]
\[Отсюда:\ \]
\[S = \frac{1}{2}ab \cdot \sin C.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{9.}}\]
\[Теорема\ синусов:\]
\[стороны\ треугольника\ \]
\[пропорциональны\ синусам\ \]
\[противоположных\ сторон.\]
\[Доказательство.\]
\[Пусть\ в\ ⊿ABC\ стороны\ \]
\[обозначены:\]
\[AB = c;BC = a;CA = b.\]
\[По\ теореме\ о\ площади\ \]
\[треугольника:\]
\[S = \frac{1}{2}ab \cdot \sin C;\]
\[S = \frac{1}{2}bc \cdot \sin A;\]
\[S = \frac{1}{2}ac \cdot \sin B.\]
\[Из\ первых\ двух\ равенств:\]
\[\frac{1}{2}ab \cdot \sin C = \frac{1}{2}bc \cdot \sin A\]
\[\frac{a}{\sin A} = \frac{c}{\sin C}.\]
\[Аналогично\ из\ второго\ \]
\[и\ третьего\ равенства:\]
\[\frac{1}{2}bc \cdot \sin A = \frac{1}{2}ac \cdot \sin B\]
\[\frac{a}{\sin A} = \frac{b}{\sin B}.\]
\[Отсюда:\]
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{10.}}\]
\[\mathbf{Теорема\ косинусов.}\]
\[квадрат\ \ стороны\ \ \]
\[треугольника\ \ равен\ \ сумме\ \]
\[квадратов\ \ двух\ \ других\ \ \]
\[сторон\ \ минус\ \ удвоенное\ \]
\[произведение\ \ этих\ \ сторон,\ \]
\[умноженное\ на\ косинус\ \ угла\ \ \]
\[между\ \ ними.\]
\[Доказательство.\]
\[Пусть\ в\ ⊿ABC\ стороны\ \]
\[обозначены:\]
\[AB = c;BC = a;CA = b.\]
\[Введём\ \ систему\ \ координат\ \ \]
\[с\ \ началом\ \ в\ \ точке\ \ A.\]
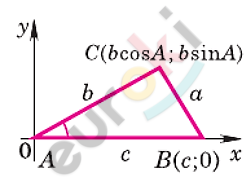
\[Тогда:\]
\[B(c;0);\]
\[C\left( b \cdot \cos A;b \cdot \sin A \right).\]
\[По\ формуле\ расстояния\ \]
\[между\ двумя\ точками:\]
\[BC^{2} = a^{2} =\]
\[= \left( b \cdot \cos A - c \right)^{2} + b^{2}\sin^{2}A =\]
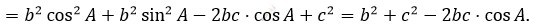
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{11.}}\]
\[Решением\ треугольника\ \ \]
\[называется\ нахождение\ \ всех\ \ \]
\[его\ \ шести\ \ элементов\ \ \]
\[(т.\ е.\ \ трёх\ \ сторон\ и\ \ трёх\ \ углов)\ \]
\[по\ \ каким - нибудь\ трём\ \ \]
\[данным\ \ элементам,\ \]
\[определяющим\ \ треугольник.\]
\[Три\ задачи\ на\ решение\ \]
\[треугольника.\]
\[Обозначения\ для\ сторон\ \]
\[треугольника\ ABC:\]
\[AB = c;BC = a;CA = b.\]
\[Задача\ 1.\]
\[Дано:\]
\[a;b;\]
\[\angle C.\]
\[Найти:\]
\[c;\]
\[\angle A;\ \angle B.\]
\[Решение.\]
\[1)\ По\ теореме\ косинусов:\]
\[c = \sqrt{a^{2} + b^{2} - 2ab \cdot \cos C}.\]
\[2)\ Пользуясь\ теоремой\ \]
\[косинусов:\]
\[\cos A = \frac{b^{2} + c^{2} - a^{2}}{2bc};\]
\[\angle A\ находим\ с\ помощью\ \]
\[таблицы\ или\ калькулятора.\]
\[3)\ \angle B = 180{^\circ} - \angle A - \angle C.\]
\[Задача\ 2.\]
\[Дано:\]
\[a;\]
\[\angle B;\ \ \angle C.\]
\[Найти:\]
\[\angle A;\]
\[b;c.\]
\[Решение.\]
\[1)\ \angle A = 180{^\circ} - \angle B - \angle C.\]
\[2)\ С\ помощью\ теоремы\ \]
\[синусов\ вычислить:\]
\[b = a \cdot \frac{\sin B}{\sin A};\ \ \ \]
\[c = a \cdot \frac{\sin C}{\sin A}.\]
\[Задача\ 3.\]
\[Дано:\]
\[a;b;c.\]
\[Найти:\]
\[\angle A;\ \angle B;\ \angle C.\]
\[Решение.\]
\[1)\ По\ теореме\ косинусов:\]
\[\cos A = \frac{b^{2} + c^{2} - a^{2}}{2bc}.\]
\[\angle A\ находим\ с\ помощью\ \]
\[таблицы\ или\ калькулятора.\]
\[2)\ Аналогично\ находим\ \angle B.\]
\[3)\ \angle C = 180{^\circ} - \angle A - \angle B.\]
\[\boxed{\mathbf{12.}}\]
\[Определить\ высоту\ предмета,\ \]
\[основание\ которого\ \]
\[недоступно.\]
\[Решение.\]
\[AH - высота\ предмета.\]
\[Если\ \ основание\ \ предмета\ \ \]
\[недоступно,\ то\ можно\ \ \]
\[поступить\ \ так:\ \ \]
\[на\ \ прямой,\ проходящей\ через\ \ \]
\[основание\ \ H\ \ предмета,\ \]
\[отметим\ \ две\ точки\ \ B\ \ и\ \ C\ \ \]
\[на\ \ определённом\ \ расстоянии\ \]
\[\ a\ \ друг\ \ от\ друга\ \ и\ \ измерим\ \ \]
\[углы\ \ ABH\ \ и\ \ ACB:\ \]
\[\angle ABH = \alpha;\ \ \ \angle ACB = \beta.\]
\[\angle ABH - внешний\ угол\ \]
\[треугольника\ ABC:\]
\[\angle A = \alpha - \beta.\]
\[По\ теореме\ синусов:\]
\[AB = \frac{a \cdot \sin\beta}{\sin(\alpha - \beta)}.\]
\[⊿ABH - прямоугольный:\]
\[AH = AB \cdot \sin\alpha.\]
\[Тогда:\]
\[AH = \frac{a \cdot \sin\alpha \cdot \sin\beta}{\sin(\alpha + \beta)}.\]
\[\boxed{\mathbf{13.}}\]
\[\mathbf{Измерение\ расстояния\ }\]
\[\mathbf{до\ недоступной\ точки.}\]
\[Решение.\]
\[На\ \ местности\ \ выберем\ \ точку\ \ \]
\[В\ \ и\ измерим\ \ длину\ \ с\ \ отрезка\ \ \]
\[\text{AB.\ \ }\]
\[Затем\ \ измерим,\ например,\ \]
\[с\ \ помощью\ \ астролябии,\ \]
\[углы\ \ A\ \ и\ \ B:\]
\[\angle A = \alpha;\ \ \angle B = \beta.\]
\[Данные\ (c;\alpha;\beta)\ позволяют\ \]
\[решить\ ⊿ABC\ и\ найти\ \]
\[искомое\ расстояние\]
\[d = AC.\]
\[Найдем\ угол\ C:\]
\[\angle C = 180{^\circ} - \alpha - \beta;\]
\[\sin C = \sin(180{^\circ} - \alpha - \beta) =\]
\[= \sin(\alpha + \beta).\]
\[По\ теореме\ синусов:\]
\[\frac{\text{AC}}{\sin B} = \frac{\text{AB}}{\sin C}.\]
\[AC = d;\ \ AB = c;\ \ \angle B = \beta:\]
\[d = \frac{c \cdot \sin\beta}{\sin(\alpha + \beta)}.\]
\[\boxed{\mathbf{14.}}\]
\[Пусть\ \overrightarrow{}\ и\ \overrightarrow{} - два\ данных\ \]
\[вектора.\]
\[Отложим\ от\ произвольной\ \]
\[точки\ O\ векторы\ \overrightarrow{\text{OA}} = \overrightarrow{a}\ и\ \]
\[\overrightarrow{\text{OB}} = \overrightarrow{b}.\]
\[Если\ векторы\ \overrightarrow{a}\ и\ \overrightarrow{b}\ \]
\[не\ являются\ \]
\[сонаправленными,\ то\ \]
\[лучи\ OA\ и\ \text{OB}\ образуют\ \angle AOB.\]
\[Градусную\ меру\ этого\ угла\ \]
\[обозначим\ буквой\ \alpha\ и\ будем\ \]
\[говорить,\ что\ угол\ между\ \]
\[векторами\ \overrightarrow{a}\ и\ \overrightarrow{b}\ равен\ \alpha.\]
\[Если\ векторы\ сонаправлены\ \]
\[или\ нулевые,\ то\ угол\ между\ \]
\[ними\ равен\ 0{^\circ}.\]
\[\boxed{\mathbf{15.}}\]
\[Два\ вектора\ называются\ \]
\[перпендикулярными,\ если\ \]
\[угол\ между\ ними\ равен\ 90{^\circ}.\]
\[\boxed{\mathbf{16.}}\]
\[\mathbf{Скалярным\ \ произведением\ \ }\]
\[\mathbf{двух\ \ векторов\ называется\ \ }\]
\[\mathbf{произведение\ }\mathbf{их\ \ длин\ \ }\]
\[\mathbf{на\ \ косинус\ угла\ \ между\ \ ними}\mathbf{.}\]
\[\boxed{\mathbf{17.}}\]
\[\textbf{а)}\ только\ тогда,\ когда\ векторы\ \]
\[перпендикулярны;\ \]
\[\textbf{б)}\ при\ \angle\overrightarrow{a}\overrightarrow{b} < 90{^\circ};\]
\[\textbf{в)}\ при\ \angle\overrightarrow{a}\overrightarrow{b} > 90{^\circ}.\]
\[\boxed{\mathbf{18.}}\]
\[Выведем\ формулу:\]
\[\overrightarrow{a} \cdot \overrightarrow{b} = x_{1}x_{2} + y_{1}y_{2}.\]
\[Пусть\ \overrightarrow{a}\ и\ \overrightarrow{b} - ненулевые\ \]
\[векторы.\]
\[Отложим\ от\ точки\ \text{O\ }векторы\]
\[\ \overrightarrow{\text{OA}} = \overrightarrow{a};\ \ \overrightarrow{\text{OB}} = \overrightarrow{b}.\]
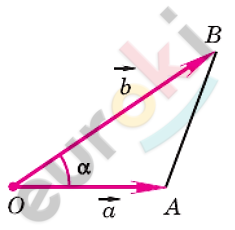
\[По\ теореме\ косинусов:\]
\[AB^{2} = OA^{2} + OB^{2} - 2OA \cdot OB \cdot \cos\alpha.\]
\[Это\ равенство\ верно\ для\ \]
\[коллинеарных\ и\ \]
\[не\ коллинеарных\ векторов.\]
\[\overrightarrow{\text{AB}} = \overrightarrow{b} - \overrightarrow{a};\ \ \ \overrightarrow{\text{OA}} = \overrightarrow{a};\ \ \overrightarrow{\text{OB}} = \overrightarrow{b}:\]
\[\left| \overrightarrow{a} - \overrightarrow{b} \right|^{2} = \left| \overrightarrow{a} \right|^{2} + \left| \overrightarrow{b} \right|^{2} - 2\overrightarrow{a}\overrightarrow{b}.\]
\[Отсюда:\]
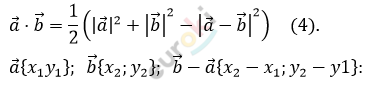
\[\left| \overrightarrow{a} \right|^{2} = x_{1}^{2} + y_{1}^{2};\]
\[\left| \overrightarrow{b} \right|^{2} = x_{2}^{2} + y_{2}^{2};\]
\[\left| \overrightarrow{b} - \overrightarrow{a} \right|^{2} =\]
\[= \left( x_{2} - x_{1} \right)^{2} + \left( y_{2} - y_{1} \right)^{2}.\]
\[Подставим\ это\ выражение\ \]
\[в\ правую\ часть\ равенства\ (4);\]
\[преобразуем:\]
\[\overrightarrow{a} \cdot \overrightarrow{b} = x_{1}x_{2} + y_{1}y_{2}.\]
\[\boxed{\mathbf{19.}}\]
\[Ненулевые\ векторы\ \overrightarrow{a}\left\{ x_{1};y_{1} \right\}\ \]
\[и\ \overrightarrow{b}\left\{ x_{2};y_{2} \right\}\ перпендикулярны\ \]
\[тогда\ и\ только\ тогда,\ когда\ \]
\[x_{1}x_{1} + y_{1}y_{2} = 0.\]
\[\boxed{\mathbf{20.}}\]
\[Косинус\ угла\ \alpha\ между\ \]
\[ненулевыми\ векторами\ \]
\[\overrightarrow{a}\left\{ x_{1};y_{1} \right\}\ и\ \overrightarrow{b}\left\{ x_{2};y_{2} \right\}\]
\[выражается\ формулой:\]
\[\cos\alpha = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^{2} + y_{1}^{2}} \cdot \sqrt{x_{2}^{2} + y_{2}^{2}}}.\]
\[Так\ как\ \overrightarrow{a} \cdot \overrightarrow{b} = \left| \overrightarrow{a} \right| \cdot \left| \overrightarrow{b} \right| \cdot \cos\alpha:\]
\[\cos\alpha = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{\left| \overrightarrow{a} \right| \cdot \left| \overrightarrow{b} \right|}.\]
\[Подставим\ сюда\ выражения\ \]
\[\left( через\ координаты\ векторов\ \overrightarrow{a}\ и\ \overrightarrow{b} \right):\]
\[\overrightarrow{a}\left\{ x_{1}y_{1} \right\};\ \ \overrightarrow{b}\left\{ x_{2};y_{2} \right\}.\]
\[\overrightarrow{a} \cdot \overrightarrow{b} = x_{1}x_{2} + y_{1}y_{2};\]
\[\left| \overrightarrow{a} \right| = \sqrt{x_{1}^{2} + y_{1}^{2}};\]
\[\left| \overrightarrow{b} \right| = \sqrt{x_{2}^{2} + y_{2}^{2}}.\]
\[Получим\ формулу:\]
\[\cos\alpha = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^{2} + y_{1}^{2}} \cdot \sqrt{x_{2}^{2} + y_{2}^{2}}}.\]
\[\boxed{\mathbf{21.}}\]
\[Свойства\ скалярного\ \]
\[произведения\ векторов.\]
\[Для\ любых\ векторов\ \overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}\ \ и\ \]
\[любого\ числа\ k\ справедливы\ \]
\[отношения:\]
\[1^{0}\text{.\ \ }{\overrightarrow{a}}^{2} \geq 0;\ \ {\overrightarrow{a}}^{2} > 0\ \ при\ \overrightarrow{a} \neq \overrightarrow{0};\]
\[2^{0}\text{.\ }\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{b} \cdot \overrightarrow{a} -\]
\[переместительный\ закон;\]
\[3^{0}\text{.\ }\left( \overrightarrow{a} + \overrightarrow{b} \right) \cdot \overrightarrow{c} = \overrightarrow{a} \cdot \overrightarrow{c} + \overrightarrow{b} \cdot \overrightarrow{c} -\]
\[распределительный\ закон.\]
\[4^{0}\text{.\ }\left( k\overrightarrow{a} \right) \cdot \overrightarrow{b} = k \cdot \left( \overrightarrow{a} \cdot \overrightarrow{b} \right) -\]
\[сочетательный\ закон.\]
\[Доказательство.\]
\[Утверждение\ 1.\]
\[Следует\ из\ формулы\ \]
\[\overrightarrow{a} \cdot \overrightarrow{a} = \left| \overrightarrow{a} \right|^{2}.\]
\[Утверждение\ 2.\]
\[Следует\ из\ определения\ \]
\[скалярного\ произведения.\]
\[Для\ утверждений\ 3\ и\ 4\ введем\ \]
\[прямоугольную\ систему\ \]
\[координат,обозначим:\]
\[\overrightarrow{a}\left\{ x_{1};y_{1} \right\};\ \ \overrightarrow{b}\left\{ x_{2};y_{2} \right\};\ \ \overrightarrow{c}\left\{ x_{3};y_{3} \right\}\]
\[Утверждение\ 3.\]
\[Используя\ формулу\]
\[\text{\ \ }\overrightarrow{a} \cdot \overrightarrow{b} = x_{1}x_{2} + y_{1}y_{2}\ получаем:\]
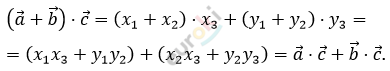
\[Утверждение\ 4.\]
\[Вектор\ k\overrightarrow{a}\ имеет\ координаты\]
\[\ \left\{ kx_{1};ky_{1} \right\}:\]
\[\left( k\overrightarrow{a} \right) \cdot \overrightarrow{b} = \left( kx_{1} \right)x_{2} + \left( ky_{1} \right)y_{2} =\]
\[= k\left( x_{1}x_{2} + y_{1}y_{2} \right) = k\left( \overrightarrow{a} \cdot \overrightarrow{b} \right).\]
\[\boxed{\mathbf{22.}}\]
\[Дано:\ \]
\[\mathrm{\Delta}ABC - равнобедренный;\]
\[\text{BN\ }и\ CK - медианы.\]
\[Доказать:\]
\[BN = CK.\]
\[Доказательство:\]
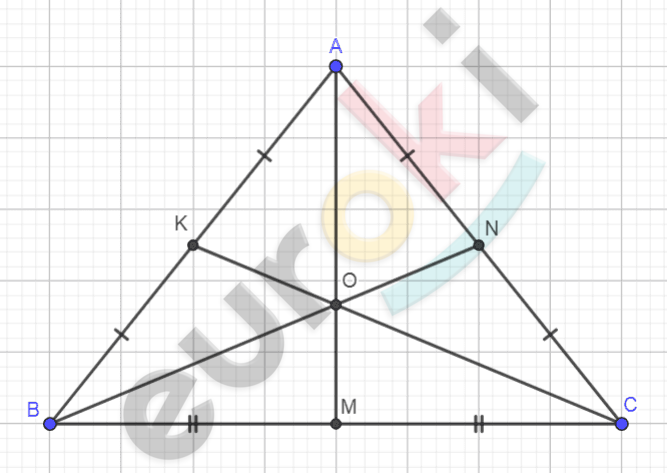
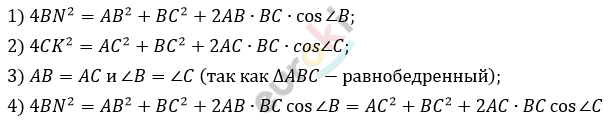
\[4BN^{2} = 4CK^{2}.\]
\[Значит:\ \]
\[CK = BN.\]
\[Что\ и\ требовалось\ доказать\text{.\ }\]











