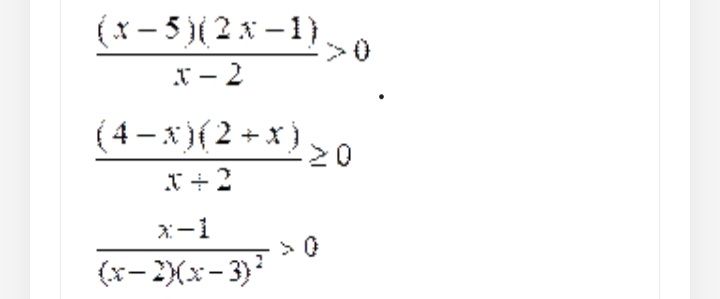
Вопрос:
\frac{x-1}{(x-2)(x-3)^2}>0
Ответ:
Решим неравенство методом интервалов:
- Найдем нули числителя и знаменателя:
- $$x-1=0 \Rightarrow x=1$$
- $$x-2=0 \Rightarrow x=2$$
- $$x-3=0 \Rightarrow x=3$$
- Отметим найденные значения на числовой прямой:
- + - +
----o--------o--------o--------o-------->
1 2 3
- Определим знаки на каждом интервале. Расставим знаки, начиная справа, учитывая, что при переходе через точку $$x=3$$, кратность которой четная, знак не меняется.
- Выберем интервалы, где выражение больше нуля ($$>0$$).
Ответ: $$x \in (1; 2) \cup (3; +\infty)$$