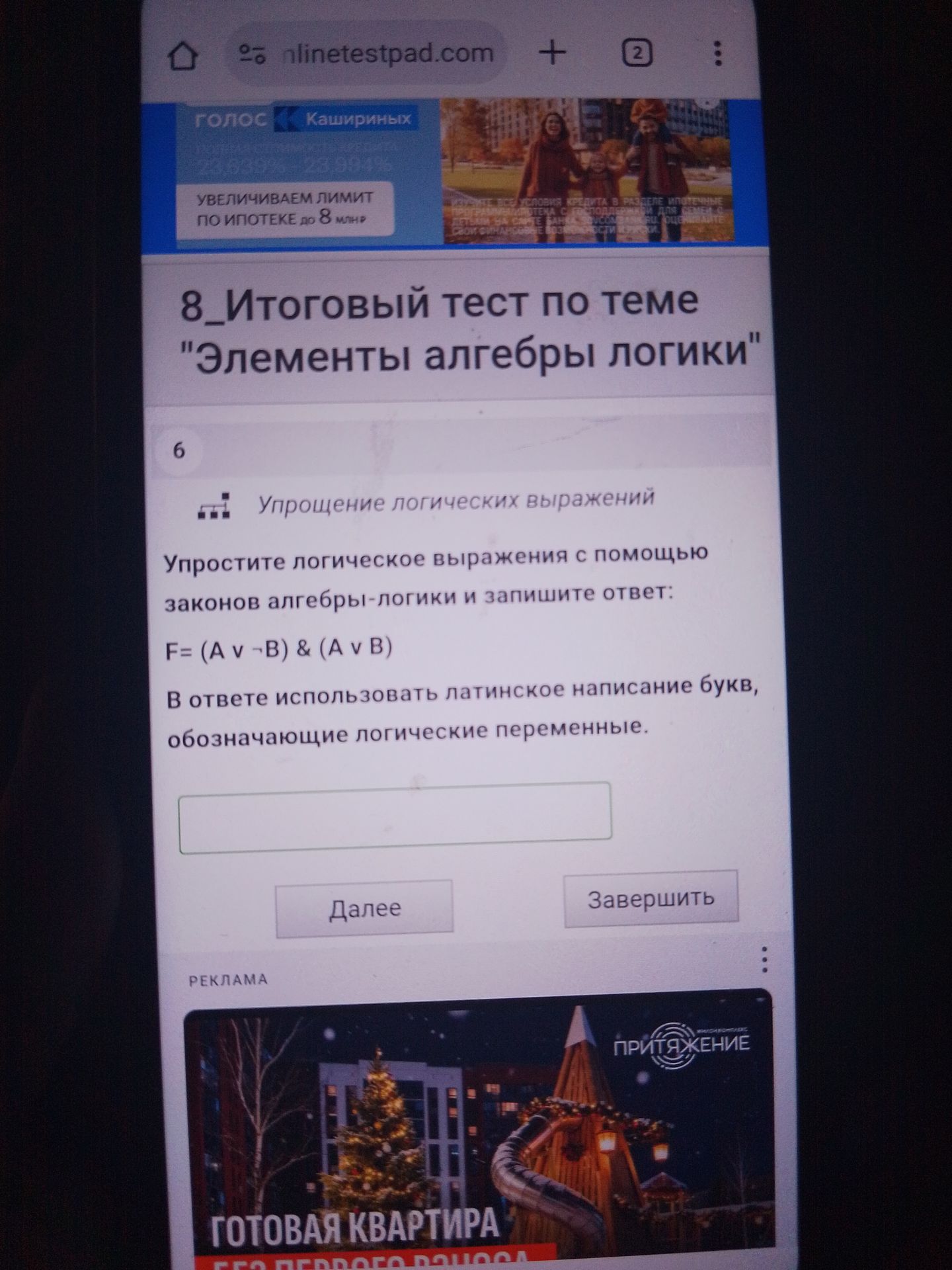
8_Итоговый тест по теме "Элементы алгебры логики" 6 Упрощение логических выражений Упростите логическое выражения с помощью законов алгебры-логики и запишите ответ: F= (A v -B) & (A v B) В ответе использовать латинское написание букв, обозначающие логические переменные.

Упростим логическое выражение $$F = (A \lor
eg B) \land (A \lor B)$$.

Используем дистрибутивный закон: $$x \land (y \lor z) = (x \land y) \lor (x \land z)$$. В нашем случае, можно рассмотреть $$A \lor B$$ как $$x$$, тогда $$ (A \lor
eg B) \land (A \lor B) = (A \lor B) \land (A \lor
eg B)$$.

Применим свойство поглощения: $$a \lor (a \land b) = a$$, если бы у нас было $$A \lor (
eg B \land B)$$, тогда можно упростить, раскрыв скобки, получим $$(A \land A) \lor (A \land B) \lor (
eg B \land A) \lor (
eg B \land B)$$.

По свойству идемпотентности $$A \land A = A$$, а также $$
eg B \land B = 0$$, тогда выражение примет вид $$A \lor (A \land B) \lor (
eg B \land A)$$.

Вынесем $$A$$ за скобки: $$A \lor (A \land (B \lor
eg B)) = A \lor (A \land 1) = A \lor A = A$$.

Следовательно, $$F = A$$.

Ответ: A