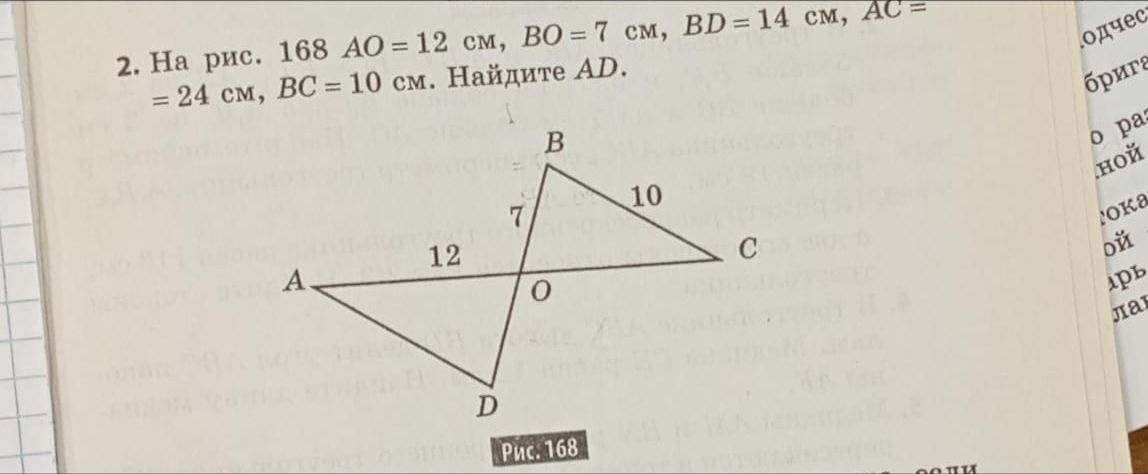
2. На рис. 168 АО = 12 см, ВО = 7 см, BD = 14 см, АС = = 24 см, ВС = 10 см. Найдите AD.

Рассмотрим треугольники $$\triangle BOC$$ и $$\triangle AOD$$.

Из условия задачи следует, что:

• $$AO = 12 \text{ см}$$,
• $$BO = 7 \text{ см}$$,
• $$BD = 14 \text{ см}$$,
• $$AC = 24 \text{ см}$$,
• $$BC = 10 \text{ см}$$.

Найдем $$OC$$ и $$OD$$.

$$AC = AO + OC$$

$$OC = AC - AO = 24 - 12 = 12 \text{ см}$$

$$BD = BO + OD$$

$$OD = BD - BO = 14 - 7 = 7 \text{ см}$$

Проверим пропорциональность сторон:

$$\frac{BO}{OD} = \frac{7}{7} = 1$$

$$\frac{OC}{AO} = \frac{12}{12} = 1$$

Т.е. стороны пропорциональны:

$$\frac{BO}{OD} = \frac{OC}{AO}$$

$$ \angle BOC = \angle AOD$$, т.к. вертикальные.

Следовательно, $$\triangle BOC \sim \triangle AOD$$ по двум пропорциональным сторонам и углу между ними.

Значит, стороны пропорциональны:

$$\frac{BC}{AD} = \frac{BO}{OD}$$

$$\frac{10}{AD} = \frac{7}{7}$$

$$\frac{10}{AD} = 1$$

$$AD = 10 \text{ см}$$

Ответ: $$AD = 10 \text{ см}$$