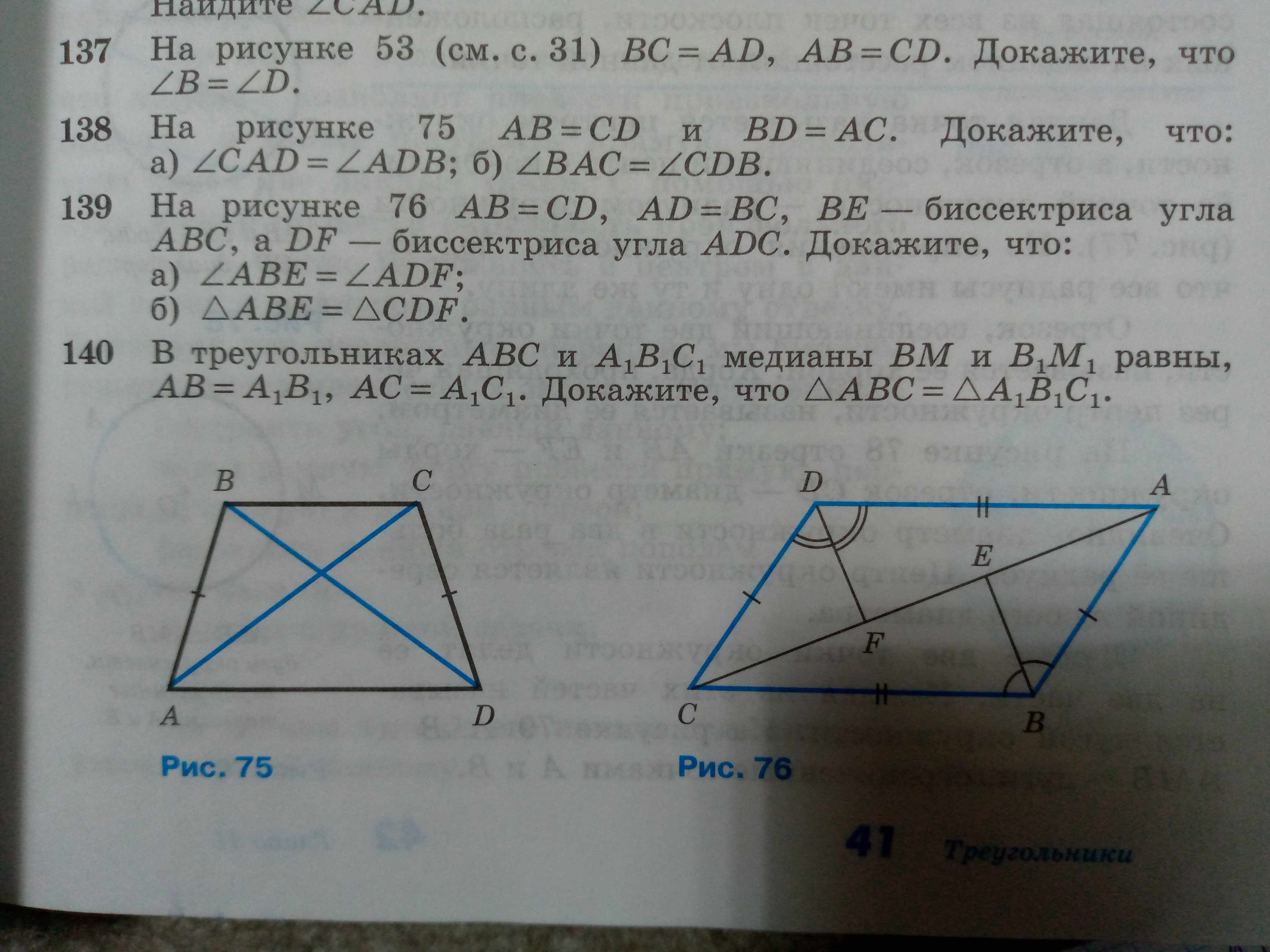
138 На рисунке 75 AB = CD и BD = АС. Докажите, что: a) ∠CAD = ∠ADB; б) ∠BAC = ∠CDB.

Рассмотрим задачу 138 с рисунком 75. a) Доказательство ∠CAD = ∠ADB: 1. Дано: AB = CD, BD = AC. 2. Рассмотрим треугольники ABD и DCA. 3. В них: AB = CD (по условию), BD = AC (по условию), AD – общая сторона. 4. Следовательно, треугольники ABD и DCA равны по трем сторонам (III признак равенства треугольников). 5. Из равенства треугольников следует равенство соответствующих углов: ∠CAD = ∠ADB. б) Доказательство ∠BAC = ∠CDB: 1. Так как треугольники ABD и DCA равны (доказано в пункте а), то ∠BAD = ∠CDA. 2. ∠BAC = ∠BAD - ∠CAD 3. ∠CDB = ∠CDA - ∠ADB 4. Учитывая, что ∠CAD = ∠ADB и ∠BAD = ∠CDA, получаем ∠BAC = ∠CDB.