Найдите четыре последовательных чётных натуральных числа, если утроенное произведение второго и четвертого чисел на 324 больше произведения первого и третьего чисел.

Ответ:

\[Пусть\ 2n - 2,\ 2n,\ 2n + 2,\ \]

\[2n + 4 - четыре\ \]

\[последовательных\ четных\]

\[натуральных\ числа.\]

\[Составим\ уравнение:\ \]

\[3 \cdot 2n(2n + 4) - 324 =\]

\[= (2n - 2)(2n + 2)\]

\[12n^{2} + 24n - 324 = 4n^{2} - 4\]

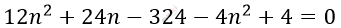
\[8n² + 24n - 320 = 0\ \ |\ :8\]

\[n^{2} + 3n - 40 = 0\]

\[D = 3^{2} - 4 \cdot 1 \cdot ( - 40) =\]

\[= 9 + 160 = 169\]

\[n_{1} = \frac{- 3 + \sqrt{169}}{2 \cdot 1} = \frac{- 3 + 13}{2} =\]

\[= \frac{10}{2} = 5.\]

\[n_{2} = \frac{- 3 - \sqrt{169}}{2 \cdot 1} = \frac{- 3 - 13}{2} =\]

\[= - \frac{16}{2} = - 8\ (не\ подходит).\]

\[2n - 2 = 2 \cdot 5 - 2 =\]

\[= 10 - 2 = 8 - первое\ число.\]

\[2n = 2 \cdot 5 = 10 - второе\ число.\]

\[2n + 2 = 2 \cdot 5 + 2 =\]

\[= 10 + 2 = 12 - третье\ число.\]

\[2n + 4 = 2 \cdot 5 + 4 =\]

\[= 10 + 4 = 14 - четвертое\ \]

\[число.\]

\[Ответ:8;10;12;14.\]