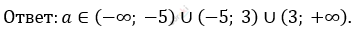Найдите все значения параметра a, при каждом из которых система уравнений (a-1)x+3y=5; 4x+(a+3)y=10 имеет единственное решение.

\[\left\{ \begin{matrix} (a - 1)x + 3y = 5\ \ \\ 4x + (a + 3)y = 10 \\ \end{matrix} \right.\ \]

\[1)\ \ a \neq 0:\ \ \ \frac{a - 1}{4} \neq \frac{3}{a + 3}\]

\[\frac{a - 1}{4} = \frac{3}{a + 3}\]

\[(a - 1)(a + 3) = 3 \cdot 4\]

\[a^{2} + 2a - 3 = 12\]

\[a^{2} + 2a - 15 = 0\]

\[D = 2^{2} - 4 \cdot 1( - 15) = 4 + 60 =\]

\[= 64\]

\[a_{1} = \frac{- 2 + \sqrt{64}}{2} = \frac{- 2 + 8}{2} = \frac{6}{2} =\]

\[= 3\]

\[a_{2} = \frac{- 2 - \sqrt{64}}{2} = \frac{- 2 - 8}{2} =\]

\[= \frac{- 10}{2} = - 5\]

\[Единственное\ решение\ при\ \]

\[любых\ a \neq 0\ и\ \ a \neq - 5.\]

\[2)\ a = 0:\ \ \]

\[\left\{ \begin{matrix} - x + 3y = 5\ \ \ \ \ \ (1)\ \\ 4x + 3y = 10\ \ \ \ (2)\ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[(2) - (1):\ \ \ 5x = 5\]

\[\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }x = 1\]

\[\left\{ \begin{matrix} x = 1\ \ \ \ \ \ \ \ \ \\ 3y = x + 5 \\ \end{matrix} \right.\ \]

\[3y = 1 + 5\]

\[3y = 6\]

\[y = 2\]

\[Единственное\ решение \Longrightarrow\]

\[\Longrightarrow (1;2).\]