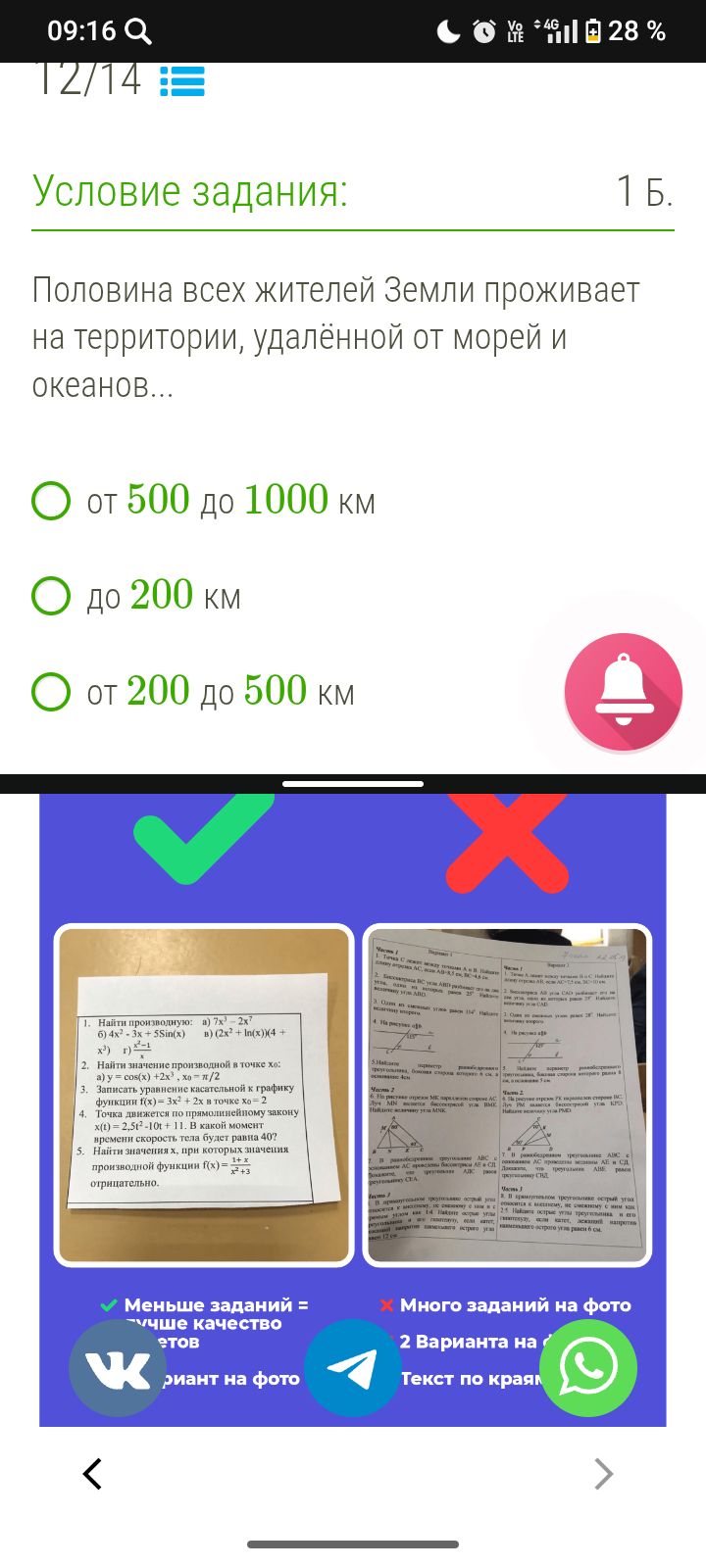
1. Найти производную: а) 7х³-2x⁷ б) 4x²-3x+5Sin(x) в) (2x²+ In(x))(4+ x³) r)2-1 x² 2. Найти значение производной в точке хо: a) y = cos(x) +2x³, χο=π/2 3. Записать уравнение касательной к графику функции f(x) = 3х² + 2х в точке хо=2 4. Точка движется по прямолинейному закону x(t)=2,5t²-10t + 11. В какой момент времени скорость тела будет равна 40? 5. Найти значения х, при которых значения производной функции f(x) = (1+ x)/(x²+3) отрицательно.

1. Найти производную:

1. $$а) y = 7x^3 - 2x^7$$$$y' = 7 \cdot 3x^2 - 2 \cdot 7x^6 = 21x^2 - 14x^6$$
2. $$б) y = 4x^2 - 3x + 5Sin(x)$$$$y' = 4 \cdot 2x - 3 + 5Cos(x) = 8x - 3 + 5Cos(x)$$
3. $$в) y = (2x^2 + ln(x))(4 + x^3)$$$$y' = (2 \cdot 2x + \frac{1}{x})(4 + x^3) + (2x^2 + ln(x))(3x^2)$$$$y' = (4x + \frac{1}{x})(4 + x^3) + (2x^2 + ln(x))(3x^2)$$
4. $$г) y = \frac{2-1}{x^2} = \frac{1}{x^2} = x^{-2}$$$$y' = -2x^{-3} = -\frac{2}{x^3}$$

2. Найти значение производной в точке $$x_0$$:

1. $$a) y = cos(x) + 2x^3, x_0 = \frac{\pi}{2}$$$$y' = -sin(x) + 2 \cdot 3x^2 = -sin(x) + 6x^2$$$$y'(\frac{\pi}{2}) = -sin(\frac{\pi}{2}) + 6(\frac{\pi}{2})^2 = -1 + 6 \cdot \frac{\pi^2}{4} = -1 + \frac{3\pi^2}{2}$$

3. Записать уравнение касательной к графику функции $$f(x) = 3x^2 + 2x$$ в точке $$x_0 = 2$$

Уравнение касательной имеет вид: $$y = f'(x_0)(x - x_0) + f(x_0)$$

Находим $$f(x_0)$$ и $$f'(x_0)$$:

$$f(x_0) = f(2) = 3 \cdot 2^2 + 2 \cdot 2 = 12 + 4 = 16$$

$$f'(x) = 6x + 2$$

$$f'(x_0) = f'(2) = 6 \cdot 2 + 2 = 12 + 2 = 14$$

Подставляем в уравнение касательной:

$$y = 14(x - 2) + 16$$

$$y = 14x - 28 + 16$$

$$y = 14x - 12$$

4. Точка движется по прямолинейному закону $$x(t) = 2,5t^2 - 10t + 11$$. В какой момент времени скорость тела будет равна 40?

Скорость тела $$v(t)$$ является производной от координаты $$x(t)$$ по времени:

$$v(t) = x'(t) = 2,5 \cdot 2t - 10 = 5t - 10$$

Нам нужно найти момент времени $$t$$, когда скорость равна 40:

$$v(t) = 40$$

$$5t - 10 = 40$$

$$5t = 50$$

$$t = 10$$

5. Найти значения $$x$$, при которых значения производной функции $$f(x) = \frac{1 + x}{x^2 + 3}$$ отрицательно.

Найдем производную функции $$f(x)$$.

$$f'(x) = \frac{(1 + x)'(x^2 + 3) - (1 + x)(x^2 + 3)'}{(x^2 + 3)^2}$$$$f'(x) = \frac{1 \cdot (x^2 + 3) - (1 + x)(2x)}{(x^2 + 3)^2}$$$$f'(x) = \frac{x^2 + 3 - 2x - 2x^2}{(x^2 + 3)^2}$$$$f'(x) = \frac{-x^2 - 2x + 3}{(x^2 + 3)^2}$$

Найдём значения $$x$$ при которых $$f'(x) < 0$$. Так как знаменатель всегда положителен, то нужно найти значения $$x$$, при которых числитель отрицателен:

$$-x^2 - 2x + 3 < 0$$

$$x^2 + 2x - 3 > 0$$

Найдем корни квадратного уравнения $$x^2 + 2x - 3 = 0$$:

$$D = 2^2 - 4 \cdot 1 \cdot (-3) = 4 + 12 = 16$$

$$x_1 = \frac{-2 + \sqrt{16}}{2} = \frac{-2 + 4}{2} = \frac{2}{2} = 1$$

$$x_2 = \frac{-2 - \sqrt{16}}{2} = \frac{-2 - 4}{2} = \frac{-6}{2} = -3$$

Так как коэффициент при $$x^2$$ положительный, то неравенство выполняется при $$x < -3$$ или $$x > 1$$

Ответ:

1.

1. $$а) y' = 21x^2 - 14x^6$$
2. $$б) y' = 8x - 3 + 5Cos(x)$$
3. $$в) y' = (4x + \frac{1}{x})(4 + x^3) + (2x^2 + ln(x))(3x^2)$$
4. $$г) y' = -\frac{2}{x^3}$$

2.

1. $$a) y'(\frac{\pi}{2}) = -1 + \frac{3\pi^2}{2}$$

3. $$y = 14x - 12$$

4. $$t = 10$$

5. $$x < -3$$ или $$x > 1$$