Определите, при каких значениях а система неравенств [4x+a<0]; [7-2x>0] имеет решение и при каких значениях не имеет решения.

Ответ:

\[\left\{ \begin{matrix} 4x + a < 0 \\ 7 - 2x > 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\left\{ \begin{matrix} 4x < - a\ \ \ \\ - 2x > - 7 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} x < - \frac{1}{4}a \\ x < \frac{2}{7}\text{\ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]

\[При\ a > 0:\]

\[система\ имеет\ решение.\]

\[При\ a < 0:\]

\[система\ имеет\ решение.\]

\[Ответ:имеет\ решение\ при\ любом\ a.\]

\[0,416 = \frac{416}{1000} = \frac{2496}{6000};\ \ \ \]

\[\frac{5}{12} = \frac{2500}{6000};\]

\[\frac{2496}{6000} < \frac{2500}{6000};\]

\[0,416 < \frac{5}{12}.\]

\[\frac{1}{6} < x < \frac{1}{2}\]

\[\frac{1}{6} = 0,1(6);\ \frac{1}{5} = 0,2.\]

\[x = 0,1777.\]

\[Ответ:0,1777.\]

\[- 10 \in R\]

\[199 \in Z\]

\[\pi \notin Q\]

\[a + 3 \leq b + 3\]

\[a \leq b.\]

\[Верные\ равенства:\]

\[a \leq b\]

\[- a + 1 \geq - b + 1\]

\[Неверные\ равенства:\]

\[\frac{1}{3}a \geq \frac{1}{3}\text{b.}\]

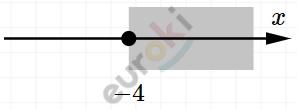
\[3 - 4x \leq 19\]

\[- 4x \leq 16\]

\[x \geq - 4.\]

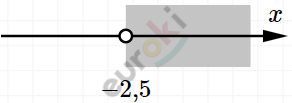
\[25 - x > 2 - 3 \cdot (x - 6)\]

\[25 - x > 2 - 3x + 18\]

\[- x + 3x > 20 - 25\]

\[2x > - 5\]

\[x > - 2,5.\]

\[\left\{ \begin{matrix} 15 - 2x < 8x\ \ \ \ \ \\ 2 + 5x > 3x - 2 \\ \end{matrix} \right.\ \text{\ \ \ \ }\left\{ \begin{matrix} - 2x - 8x < - 15\ \ \\ 5x - 3x > - 2 - 2 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} - 10x < - 15 \\ 2x > - 4\ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x > 1,5 \\ x > - 2 \\ \end{matrix} \right.\ \]

\[Ответ:x > 1,5.\]

\[l = (20 \pm 0,05)\ м.\]

\[19,95 \leq l \leq 20,05\]

\[Длина\ 20,1\ м\ не\ удовлетворяет\ условию.\]

\[Ответ:нет.\]

\[\frac{6 - 15x}{5} - \frac{6 - 5x}{2} < 0\]

\[2 \cdot (6 - 15x) - 5 \cdot (6 - 5x) < 0\]

\[12 - 30x - 30 + 25x < 0\]

\[- 5x - 18 < 0\]

\[- 5x < 18.\]

\[x > - \frac{18}{5}\]

\[x > - 3,6.\]

\[x_{наим} = - 3.\]

\[Ответ:\ - 3.\]

\[S = a \cdot b;\ \ a = 3\ см;\ \ b = \sqrt{2}\ см.\]

\[S = 3 \cdot \sqrt{2}.\]

\[1,4 < \sqrt{2} < 1,5\]

\[4,2 < S < 4,5.\]

\[a^{2} + b^{2} \geq \frac{(a + b)^{2}}{2}\]

\[2 \cdot \left( a^{2} + b^{2} \right) \geq (a + b)^{2}\]

\[2a^{2} + 2b^{2} \geq a^{2} + 2ab + b^{2}\]

\[a^{2} - 2ab + b^{2} \geq 0\]

\[(a - b)^{2} \geq 0\ при\ любых\ значениях\ \]

\[переменной.\]

\[Что\ и\ требовалось\ доказать.\]