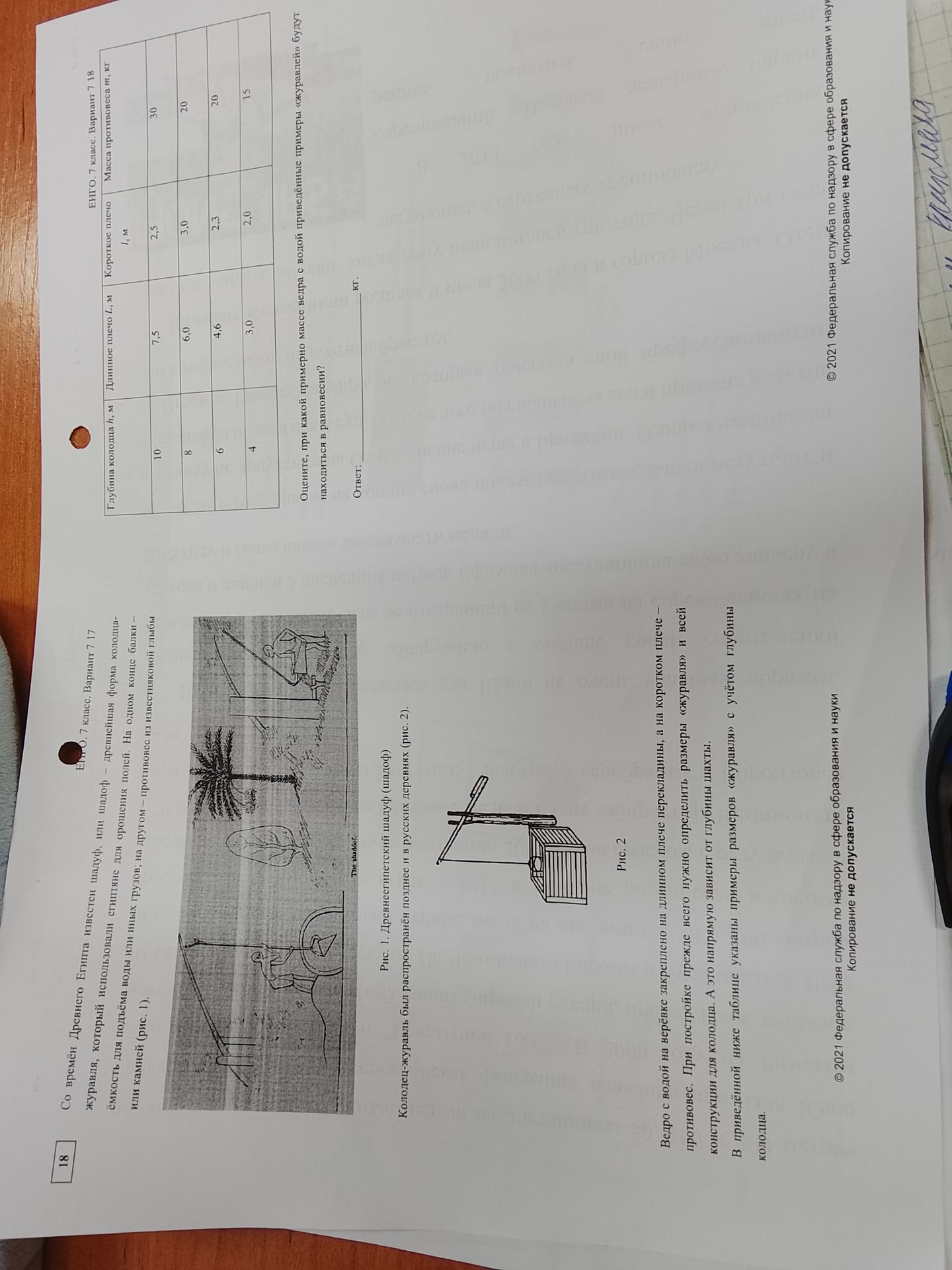
Оцените, при какой примерно массе ведра с водой приведённые примеры «журавлей» будут находиться в равновесии?

Для оценки массы ведра с водой, при которой журавль будет находиться в равновесии, необходимо рассмотреть условие равновесия рычага:

$$L_1 \cdot m_1 = L_2 \cdot m_2$$, где

$$L_1$$ - длина длинного плеча,

$$m_1$$ - масса ведра с водой,

$$L_2$$ - длина короткого плеча,

$$m_2$$ - масса противовеса.

Выразим массу ведра с водой:

$$m_1 = \frac{L_2 \cdot m_2}{L_1}$$

Рассмотрим первый случай (глубина колодца 10 м):

$$m_1 = \frac{2,5 \cdot 30}{7,5} = 10 \text{ кг}$$.

Рассмотрим второй случай (глубина колодца 8 м):

$$m_1 = \frac{3,0 \cdot 20}{6,0} = 10 \text{ кг}$$.

Рассмотрим третий случай (глубина колодца 6 м):

$$m_1 = \frac{2,3 \cdot 20}{4,6} = 10 \text{ кг}$$.

Рассмотрим четвертый случай (глубина колодца 4 м):

$$m_1 = \frac{2,0 \cdot 15}{3,0} = 10 \text{ кг}$$.

Из расчетов видно, что масса ведра с водой примерно равна 10 кг.

Ответ: 10 кг.