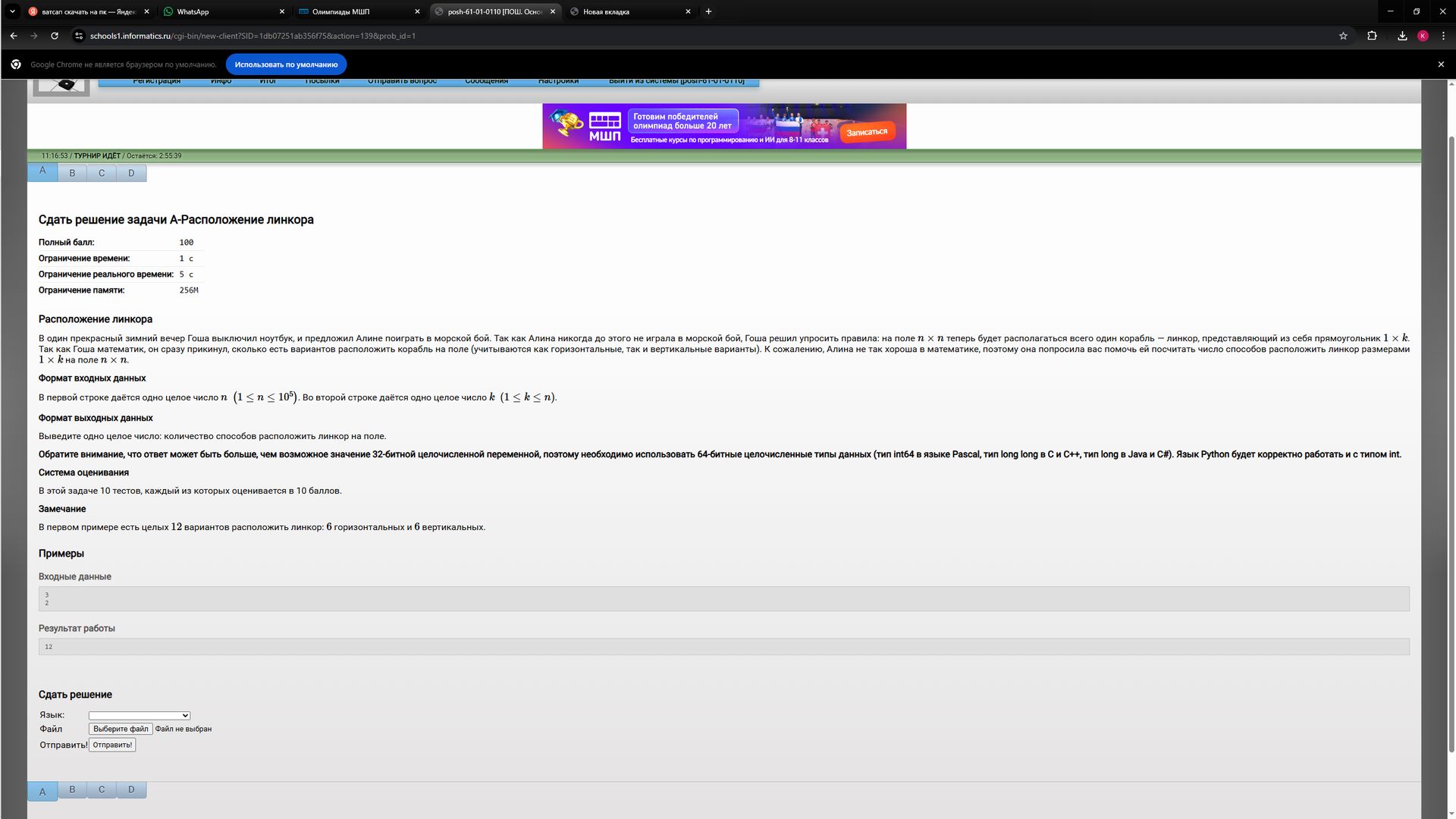
Сдать решение задачи А-Расположение линкора Полный балл: 100 Ограничение времени: 1 c Ограничение реального времени: 5 с Ограничение памяти: 256M Расположение линкора В один прекрасный зимний вечер Гоша выключил ноутбук, и предложил Алине поиграть в морской бой. Так как Алина никогда до этого не играла в морской бой, Гоша решил упростить правила: на поле n x n теперь будет располагаться всего один корабль – линкор, представляющий из себя прямоугольник 1 х k. Так как Гоша математик, он сразу прикинул, сколько есть вариантов расположить корабль на поле (учитываются как горизонтальные, так и вертикальные варианты). К сожалению, Алина не так хороша в математике, поэтому она попросила вас помочь ей посчитать число способов расположить линкор размерами 1 х k на поле n х n. Формат входных данных В первой строке даётся одно целое число n (1 ≤ n ≤ 105). Во второй строке даётся одно целое число k (1 ≤ k ≤ n). Формат выходных данных Выведите одно целое число: количество способов расположить линкор на поле. Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в С и С++, тип long в Java и С#). Язык Python будет корректно работать и с типом int. Система оценивания В этой задаче 10 тестов, каждый из которых оценивается в 10 баллов. Замечание В первом примере есть целых 12 вариантов расположить линкор: 6 горизонтальных и 6 вертикальных. Примеры Входные данные 3 2 Результат работы 12

n = int(input())
k = int(input())
result = 2 * n * (n - k + 1)
print(result)