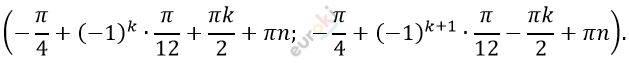Решебник по алгебре и начала математического анализа 10 класс Алимов Задание 1572

\[\boxed{\mathbf{1572}\mathbf{.}}\]

\[\left\{ \begin{matrix} 6\sin x \bullet \cos y + 2\cos x \bullet \sin y = - 3 \\ 5\sin x \bullet \cos y - 3\cos x \bullet \sin y = 1\ \ \ \\ \end{matrix} \right.\ \]

\[u = \cos x \bullet \sin y;v = \cos y \bullet \sin x:\]

\[\left\{ \begin{matrix} 6v + 2u = - 3 \\ 5v - 3u = 1\ \ \ \\ \end{matrix} \right.\ \text{\ \ }\]

\[\left\{ \begin{matrix} u = - \frac{3}{2} - 3v \\ 5v - 3u = 1\ \ \\ \end{matrix} \right.\ \]

\[5v - 3\left( - \frac{3}{2} - 3v \right) = 1\]

\[5v + \frac{9}{2} + 9v = 1\]

\[14v = 1 - 4,5\]

\[14v = - \frac{7}{2}\]

\[v = - \frac{1}{4};\]

\[u = - \frac{3}{2} - 3 \bullet \left( - \frac{1}{4} \right) =\]

\[= \frac{- 6 + 3}{4} = - \frac{3}{4}.\]

\[Получим:\]

\[\left\{ \begin{matrix} \cos x \bullet \sin y = - \frac{3}{4} \\ \cos y \bullet \sin x = - \frac{1}{4} \\ \end{matrix} \right.\ ( + )\]

\[\cos x \bullet \sin y + \cos y \bullet \sin x = - \frac{3}{4} - \frac{1}{4}\]

\[\sin(x + y) = - 1\]

\[x + y = - \arcsin 1 + 2\pi n\]

\[x + y = - \frac{\pi}{2} + 2\pi n\]

\[x = - \frac{\pi}{2} + 2\pi n - y.\]

\[\left\{ \begin{matrix} \cos x \bullet \sin y = - \frac{3}{4} \\ \cos y \bullet \sin x = - \frac{1}{4} \\ \end{matrix} \right.\ ( - )\]

\[\cos y \bullet \sin x - \cos x \bullet \sin y = - \frac{1}{4} + \frac{3}{4}\]

\[\sin(x - y) = \frac{1}{2}\]

\[x - y = ( - 1)^{k} \bullet \arcsin\frac{1}{2} + \pi k\]

\[x - y = ( - 1)^{k} \bullet \frac{\pi}{6} + \pi k.\]

\[Подставим\ x:\]

\[- \frac{\pi}{2} + 2\pi n - y - y = ( - 1)^{k} \bullet \frac{\pi}{6} + \pi k\]

\[- 2y = \frac{\pi}{2} + ( - 1)^{k} \bullet \frac{\pi}{6} + \pi k - 2\pi n\]

\[y = - \frac{\pi}{4} + ( - 1)^{k + 1} \bullet \frac{\pi}{12} - \frac{\text{πk}}{2} + \pi n;\]

\[x = - \frac{\pi}{2} + 2\pi n + \frac{\pi}{4} - ( - 1)^{k + 1} \bullet \frac{\pi}{12} + \frac{\text{πk}}{2} - \pi n\]

\[x = - \frac{\pi}{4} + ( - 1)^{k} \bullet \frac{\pi}{12} + \frac{\text{πk}}{2} + \pi n.\]

\[Ответ:\ \ \]