Решебник по алгебре 11 класс Никольский Параграф 8. Уравнения-следствия Задание 19

\[\boxed{\mathbf{19.}}\]

\[\textbf{а)}\log_{2}{\cos{2x}} = \log_{2}{\cos x}\]

\[\cos{2x} = \cos x\]

\[2\cos^{2}x - 1 = \cos x\]

\[2\cos^{2}x - \cos x - 1 = 0\]

\[\cos x = t:\]

\[2t^{2} - t - 1 = 0\]

\[D = 1 + 8 = 9\]

\[t_{1} = \frac{1 + 3}{4} = 1;\]

\[t_{2} = \frac{1 - 3}{4} = - \frac{1}{2}.\]

\[1)\cos x = 1\]

\[x = 2\pi n.\]

\[2)\cos x = - \frac{1}{2}\]

\[x = \pm \frac{2\pi}{3} + 2\pi n.\]

\[Проверка\ показала,\ что\ x =\]

\[= 2\pi n - корень\ уравнения.\]

\[Ответ:\ x = 2\pi n.\]

\[\textbf{б)}\log_{\frac{1}{2}}{\cos{2x}} =\]

\[= \log_{\frac{1}{2}}\left( \cos x + \sin x \right)\]

\[\cos{2x} = \cos x + \sin x\]

\[\text{co}s^{2}x - \sin^{2}x = \cos{x + \sin x}\]

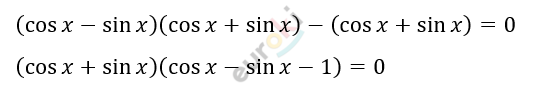
\[1)\cos x + \sin x = 0\]

\[\frac{\cos x}{\cos x} + \frac{\sin x}{\cos x} = 0\]

\[1 + tg\ x = 0\]

\[tg\ x = - 1\]

\[x = - \frac{\pi}{4} + \pi n.\]

\[2)\cos x - \sin x = 1\ \ \ |\ :\sqrt{2}\]

\[\frac{1}{\sqrt{2}}\cos x - \frac{1}{\sqrt{2}}\sin x = \frac{1}{\sqrt{2}}\]

\[\cos\left( \frac{\pi}{4} \right)\cos x - \sin\left( \frac{\pi}{4} \right)\sin x =\]

\[= \frac{1}{\sqrt{2}}\]

\[\cos\left( x + \frac{\pi}{4} \right) = \frac{1}{\sqrt{2}}\]

\[x + \frac{\pi}{4} = \frac{\pi}{4} + 2\pi n;\]

\[x + \frac{\pi}{4} = - \frac{\pi}{4} + 2\pi n;\]

\[x_{1} = 2\pi n;\]

\[x_{2} = - \frac{\pi}{2} + 2\pi n.\]

\[Проверка\ показала,\ что\ корнем\ \]

\[является\ x = 2\pi n.\]

\[Ответ:x = 2\pi n.\]

\[\textbf{в)}\log_{\frac{1}{3}}{\cos{2x}} =\]

\[= \log_{\frac{1}{3}}\left( \cos x - \sin x \right)\]

\[\cos{2x} = \cos x - \sin x\]

\[\text{co}s^{2}x - sin^{2}x = \cos x - \sin x\]

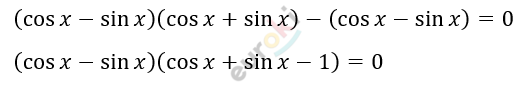
\[1)\cos x - \sin x = 0\]

\[\frac{\cos x}{\cos x} - \frac{\sin x}{\cos x} = 0\]

\[1 - tg\ x = 0\]

\[tg\ x = 1\]

\[x = \frac{\pi}{4} + \pi n.\]

\[2)\cos x + \sin x = 1\ \ \ \ |\ :\sqrt{2}\]

\[\frac{1}{\sqrt{2}}\cos x + \frac{1}{\sqrt{2}}\sin x = \frac{1}{\sqrt{2}}\]

\[\cos\left( \frac{\pi}{4} \right)\cos x + \sin\left( \frac{\pi}{4} \right)\sin x =\]

\[= \frac{1}{\sqrt{2}}\]

\[\cos\left( x - \frac{\pi}{4} \right) = \frac{1}{\sqrt{2}}\]

\[x - \frac{\pi}{4} = \frac{\pi}{4} + 2\pi n;\]

\[x - \frac{\pi}{4} = - \frac{\pi}{4} + 2\pi n;\]

\[x_{1} = 2\pi n;\]

\[x_{2} = \frac{\pi}{2} + 2\pi n.\]

\[Проверка\ показала,\ что\ x =\]

\[= 2\pi n - корень\ уравнения.\]

\[Ответ:\ x = 2\pi n.\]

\[\textbf{г)}\log_{0,2}{\cos{2x}} =\]

\[= \log_{0,2}\left( \sin x - \cos x \right)\]

\[\cos{2x} = \sin x - \cos x\]

\[\text{co}s^{2}x - sin^{2}x =\]

\[= - (\cos x - \sin x)\]

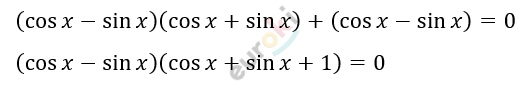
\[1)\cos x - \sin x = 0\]

\[\frac{\cos x}{\cos x} - \frac{\sin x}{\cos x} = 0\]

\[1 - tg\ x = 0\]

\[tg\ x = 1\]

\[x = \frac{\pi}{4} + \pi n.\]

\[2)\cos x + \sin x = - 1\ \ \ \ |\ :\sqrt{2}\]

\[\frac{1}{\sqrt{2}}\cos x + \frac{1}{\sqrt{2}}\sin x = - \frac{1}{\sqrt{2}}\]

\[\cos\left( \frac{\pi}{4} \right)\cos x + \sin\left( \frac{\pi}{4} \right)\sin x =\]

\[= - \frac{1}{\sqrt{2}}\]

\[\cos\left( x - \frac{\pi}{4} \right) = - \frac{1}{\sqrt{2}}\]

\[x - \frac{\pi}{4} = \frac{3\pi}{4} + 2\pi n;\]

\[x - \frac{\pi}{4} = - \frac{3\pi}{4} + 2\pi n;\]

\[x_{1} = \pi + 2\pi n;\]

\[x_{2} = - \frac{\pi}{2} + 2\pi n.\]

\[Проверка\ показала,\ что\ x =\]

\[= \pi + 2\pi n - корень\ уравнения.\]

\[Ответ:\ x = \pi + 2\pi n.\]