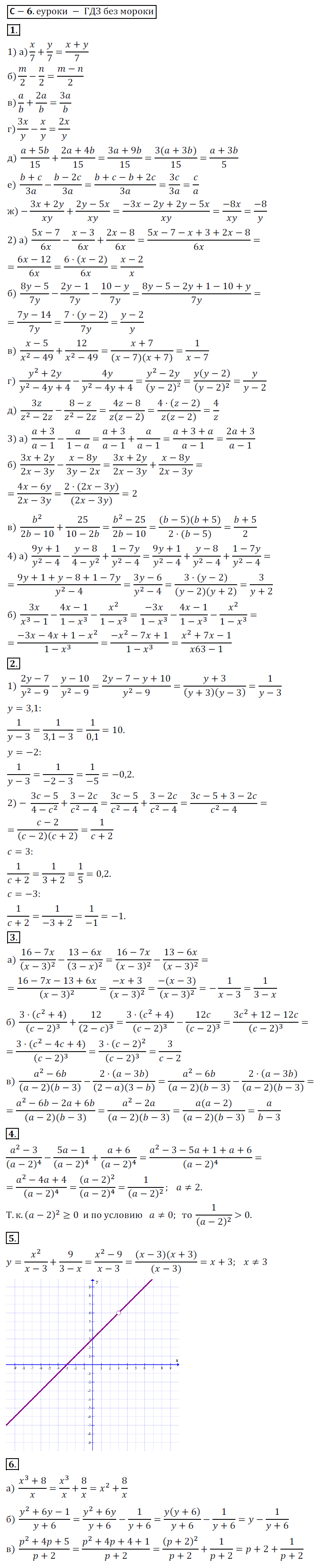ГДЗ по алгебре 8 класс Жохов дидактические материалы С-6(6). Сложение и вычитание дробей с одинаковыми знаменателями | Номер Вариант 1

Условие:

1. Выполните сложение и вычитание дробей:

1) а) x/7+y/7;

б) m/2-n/2;

в) a/b+2a/b;

г) 3x/y-x/y;

д) (a+5b)/15+(2a+4b)/15;

е) (b+c)/3a-(b-2c)/3a;

ж) –(3x+2y)/xy+(2y-5x)/xy;

2) а) (5x-7)/6x-(x-3)/6x+(2x-8)/6x;

б) (8y-5)/7y-(2y-1)/7y-(10-y)/7y;

в) (x-5)/x^2-49)+12/(x^2-49);

г) (y^2+2y)/(y^2-4y+4)-4y/(y^2-4y+4);

д) 3z/(z^2-2z)-(8-z)/(z^2-2z);

3) а) (a+3)/(a-1)-a/(1-a);

б) (3x+2y)/(2x-3y)-(x-8y)/(3y-2x);

в) b^2/(2b-10)+25/(10-2b);

4) а) (9y+1)/(y^2-4)-(y-8)/(4-y^2)+(1-7y)/(y^2-4);

б) 3x/(x^2-1)-(4x-1)/(1-x^2)-x^2/(1-x^2).

2. Найдите значение выражения

1) (2y-7)/(y^2-9)-(y-10)/(y^2-9) при y=3,1; y=-2;

2) –(3x-5)/(4-c^2)+(3-2c)/(c^2-4) при c=3; c=-3.

3. Представьте в виде дроби выражение

а) (16-7x)/(x-3)^2-(13-6x)/(3-x)^2;

б) 3*(c^2+4)/(c-2)^3+12c/(2-c)^3;

в) (a^2-6b)/((a-2)(b-3))-(2*(a-3b))/((2-a)(3-b)).

4. Докажите, что выражение (a^2-3)/(a-2)^4-(2a-1)/(a-2)^4+(a+6)/(a-2)^4 при всех a≠2 принимает отрицательные значения.

5. Постройте график функции y=x^2/(x-3)+9/(3-x).

6. Представьте в виде суммы или разности целого выражения и дроби дробь:

а) (x^3+8)/x;

б) (y^2+6y-1)/(y+6);

в) (p^2+4p+5)/(p+2).