Решебник по алгебре 9 класс Макарычев Задание 331

 

\[\boxed{\text{331\ (331).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ 2 \cdot (x - 18)(x - 19) > 0\]

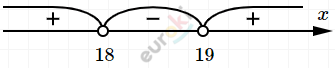
\[x \in ( - \infty;18) \cup (19; + \infty)\text{.\ }\]

\[\textbf{б)} - 4 \cdot (x + 0,9)(x - 3,2) < 0\]

\[(x + 0,9)(x - 3,2) > 0\]

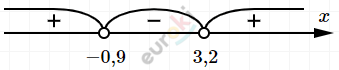
\[x \in ( - \infty;\ - 0,9) \cup (3,2;\ + \infty).\]

\[\textbf{в)}\ (7x + 21)(x - 8,5) \leq 0\]

\[7 \cdot (x + 3)(x - 8,5) \leq 0\]

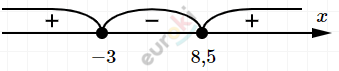
\[x \in \lbrack - 3;8,5\rbrack.\]

\[\textbf{г)}\ (8 - x)(x - 0,3) \geq 0\]

\[(x - 0,3)(x - 8) \leq 0\]

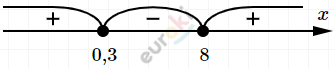
\[x \in \lbrack 0,3;8\rbrack.\]

\[\boxed{\text{331.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[\frac{1}{x^{3} - x^{2} + x - 1} + \frac{4x^{2} + 21}{x^{3} + x^{2} + x + 1} =\]

\[= \frac{4x^{3} - 3x^{2} + 14x - 4}{x^{4} - 1};\]

\[x^{4} - 1 =\]

\[= (x + 1)\left( x^{3} - x^{2} + x - 1 \right) =\]

\[= (x - 1)\left( x^{3} + x^{2} + x + 1 \right);\]

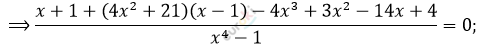
\[ОДЗ:\ \ \ x \neq \pm 1.\]

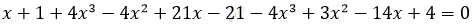
\[- x^{2} + 8x - 16 = 0\]

\[x^{2} - 8x + 16 = 0\]

\[(x - 4)^{2} = 0 \Longrightarrow x = 4.\]

\[Ответ:x = 4.\]