Алгебра
Английский
Биология
География
Геометрия
Русский
История
Обществознание
Физика
Химия
Информатика
Литература
МатематикаГДЗ по геометрии 11 класс. Атанасян ФГОС 850
850
\[\boxed{\mathbf{850.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
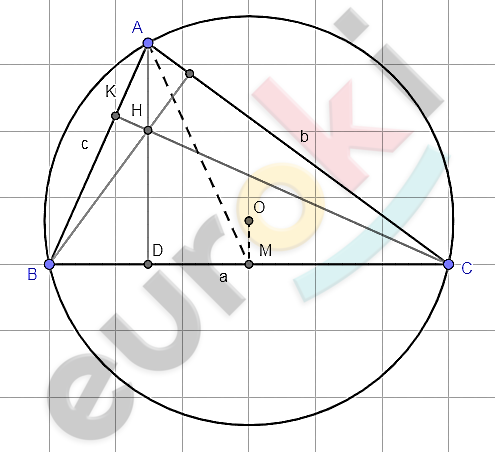
\[Дано:\ \ \]
\[\mathrm{\Delta}ABC;\ \ \]
\[AB = c;\ \ BC = a;\ \ CA = b;\ \]
\[\text{\ r\ }и\ R - радиусы\ вписанной\ и\ \]
\[описанной\ окружностей;\ \ \]
\[S - площадь;\ \]
\[\ O - центр\ описанной\ \]
\[окружности;\ \ \]
\[H - точка\ пересечения\ высот;\ \]
\[\text{\ AD\ }и\ AM - высота\ и\ медиана.\]
\[\ Доказательство:\]
\[\textbf{а)}\ По\ теореме\ синусов\ \frac{b}{\sin B} =\]
\[= \frac{a}{\sin A} = 2R:\ \]
\[a = 2R \bullet \sin A;\]
\[b = 2R \bullet \sin B;\]
\[a + b = 2R\left( \sin A + \sin B \right) =\]
\[= 4R \bullet \sin\frac{A + B}{2} \bullet \cos\frac{|A - B|}{2}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ a - b = 2R\left( \sin A - \sin B \right) =\]
\[= 4R \bullet \cos\frac{A + B}{2} \bullet \sin\frac{|A - B|}{2}\text{.\ }\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{в)}\frac{|a - b|}{a + b} =\]
\[= \frac{4R \bullet \sin\frac{A + B}{2} \bullet \cos\frac{|A - B|}{2}}{4R \bullet \cos\frac{A + B}{2} \bullet \sin\frac{|A - B|}{2}} =\]
\[= \frac{\text{tg}\frac{|A - B|}{2}}{\text{tg}\frac{A + B}{2}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{г)}\ \ По\ теореме\ косинусов -\]
\[b^{2} = a^{2} + c^{2} - 2ac \bullet \cos B:\]
\[ac \bullet \cos B - bc \bullet \cos A =\]
\[= \frac{a^{2} + c^{2} - b^{2}}{2} - \frac{b^{2} + c^{2} - a^{2}}{2} =\]
\[= a^{2} - b^{2}\]
\[\frac{a^{2} - b^{2}}{c} = a \bullet \cos B - b \bullet \cos A.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{д)}\ По\ теореме\ синусов:\]
\[a + b + c =\]
\[= 2R\left( \sin A + \sin B + \sin C \right).\]
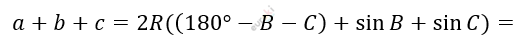
\[= 2R\left( \left( \sin B + C \right) + \sin B + \sin C \right) =\]
\[= 2R(\left( \sin B + C \right) + \sin B + \sin{C)} =\]
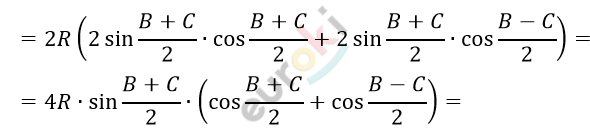
\[= 4R \bullet \cos\frac{A}{2} \bullet \left( 2\cos\frac{B}{2} + 2\cos\frac{C}{2} \right) =\]
\[= 8R \bullet \cos\frac{A}{2} \bullet \cos\frac{B}{2} \bullet \cos\frac{C}{2}\ \]
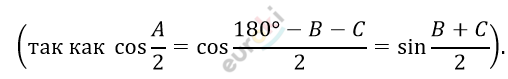
\(Что\ и\ требовалось\ доказать.\ \)=
\[\textbf{е)}\ \angle C = 180{^\circ} - \angle A - \angle B:\]
\[\cos C = - \cos(A + B);\]
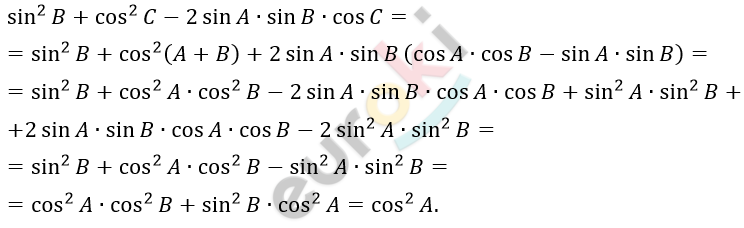
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{ж)}\frac{c}{\sin C} = 2R \rightarrow \sin C = \frac{c}{2R}:\]
\[S = \frac{\text{ab}}{2} \bullet \sin C = bR \bullet \sin C;\]
\[S = pr = \frac{a + b + c}{2}r =\]
\[= bR \bullet \sin A \bullet \sin C;\]
\[a = 2R \bullet \sin A;\ b = 2R \bullet \sin B;\]
\[r = \frac{2bR \bullet \sin A \bullet \sin C}{a + b + c} =\]
\[= \frac{4R^{2} \bullet \sin A \bullet \sin B \bullet \sin C}{a + b + c};\]
\[\sin{2a} =\]
\[= 2\sin a \bullet \cos a\text{\ \ }и\ \ a + b + c =\]
\[= 8R \bullet \cos\frac{A}{2} \bullet \cos\frac{B}{2} \bullet \cos\frac{C}{2}.\]
\[Значит:\]
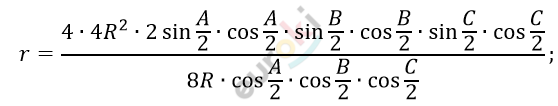
\[r = 4R \bullet \sin\frac{A}{2} \bullet \sin\frac{B}{2} \bullet \sin\frac{C}{2}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{з)}\ r = 4R \bullet \sin\frac{B}{2} \bullet \sin\frac{C}{2} \bullet \sin\frac{A}{2};\ \ \]
\[a = 2R \bullet \sin a\ \]
\[\left( так\ как\sin{2a} = 2\sin a \bullet \cos a \right);\]
\[r = \frac{2a \bullet \sin\frac{B}{2} \bullet \sin\frac{C}{2} \bullet \sin\frac{A}{2}}{\sin A} =\]
\[= \frac{2a \bullet \sin\frac{B}{2} \bullet \sin\frac{C}{2} \bullet \sin\frac{A}{2}}{2\sin{\frac{A}{2} \bullet \cos\frac{A}{2}}} =\]
\[= \frac{a \bullet \sin\frac{B}{2} \bullet \sin\frac{C}{2}}{\cos\frac{A}{2}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{и)}\ \angle DAB = 90{^\circ} - \angle B.\]
\[В\ \mathrm{\Delta}AHK:\ \ \ \]
\[AH = \frac{\text{AK}}{\cos{\angle DAB}} =\]
\[= \frac{\text{AK}}{\sin(90{^\circ} - \angle B)} = \frac{\text{AK}}{\sin B}.\]
\[По\ теореме\ синусов:\]
\[\cos A = \frac{b^{2} + c^{2} - a^{2}}{2bc};\]
\[AK = b \bullet \cos A.\]
\[Отсюда\ \left( S = \frac{1}{2}ac \bullet \sin B \right):\]
\[AH = \frac{b \bullet \cos A}{\sin B} = \frac{b^{2} + c^{2} - a^{2}}{2c \bullet \sin B} =\]
\[= \frac{a\left( b^{2} + c^{2} - a^{2} \right)}{4S}.\]
\[Что\ и\ требовалось\ доказать.\]
\[к)\ OM - серединный\ \]
\[перпендикуляр\ к\ стороне\ \text{BC.}\]
\[По\ теореме\ косинусов\ в\ \mathrm{\Delta}OCH:\ \]
\[OH^{2} =\]
\[= OC^{2} + CH^{2} - 2CO \bullet CH \bullet \cos{\angle OCH};\]
\[\angle MOC = \angle A\ (так\ как\ \angle BOC -\]
\[центральный\ угол,\ если\ \]
\[провести\ описанную\ \]
\[окружность\ \mathrm{\Delta}ABC);\]
\[\angle BCH = 90{^\circ} - \angle B;\]
\[CH = \frac{c\left( a^{2} + b^{2} - c^{2} \right)}{4S}\ \]
\[(см.\ пункт\ и);\]
\[OC = R;\ \ \ \angle OCH =\]
\[= 90{^\circ} - \angle B - \angle A;\]
\[\cos{\angle OCH} =\]
\[= \cos{(90{^\circ} - \angle B - \angle A}) =\]
\[= \sin(A + B) = \sin{\angle C};\]
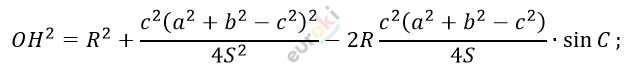
\[2S = ab \bullet \sin C.\]
\[Тогда:\]
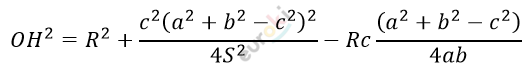
\[R = \frac{\text{abc}}{4S}\]
\[S = \frac{\text{abc}}{4R}.\]
\[Получаем:\]
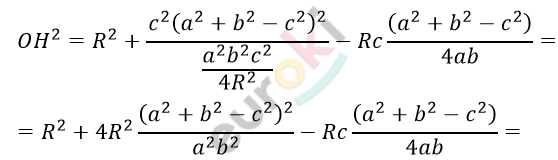
\[9R^{2} - a^{2} - b^{2} - c^{2}.\]
\[Что\ и\ требовалось\ доказать.\]
\[л)\ Пусть\ b > c;\ \ \ BD = c \bullet \cos B:\]
\[b^{2} = c^{2} + a^{2} - 2ac \bullet \cos B\ \]
\[(по\ теореме\ косинусов);\]
\[c \bullet \cos B = \frac{c^{2} + a^{2} - b^{2}}{2a};\]
\[DM = \frac{a}{2} - \frac{c^{2} + a^{2} - b^{2}}{2a} =\]
\[= \frac{b^{2} - c^{2}}{2a}.\]
\[Что\ и\ требовалось\ доказать.\]
\[Параграф\ 3.\ Теоремы\ Менелая\ и\ Чевы\]
