Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 1117
Задание 1117
\[\boxed{\mathbf{1117.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\textbf{а)}\ Рисунок\ по\ условию\ задачи:\]
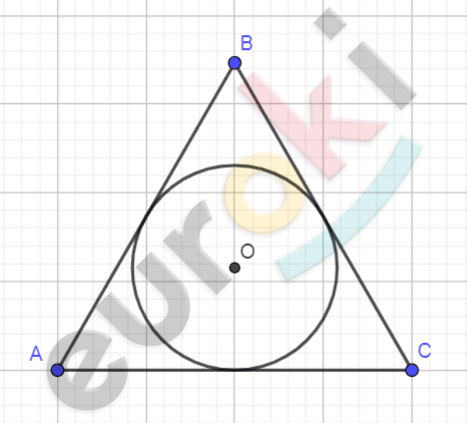
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равносторонний;\]
\[AB = a.\]
\[\mathbf{Найти:}\]
\[S_{круга} - ?\]
\[\mathbf{Решение.}\]
\[1)\ a_{3} = 2R \bullet \sin\frac{180{^\circ}}{3} =\]
\[= 2R \bullet \sin{60{^\circ}} = 2R \bullet \frac{\sqrt{3}}{2} = R\sqrt{3};\]
\[R = \frac{a_{3}}{\sqrt{3}} = \frac{a}{\sqrt{3}}.\]
\[2)\ r = R \bullet \cos\frac{180{^\circ}}{3} =\]
\[= R \bullet \cos{60{^\circ}} = \frac{a}{\sqrt{3}} \bullet \frac{1}{2} = \frac{a}{2\sqrt{3}}.\]
\[3)\ S = \pi r^{2} = \pi\left( \frac{a}{2\sqrt{3}} \right)^{2} = \frac{\pi a^{2}}{12}.\]
\[Ответ:S = \frac{\pi a^{2}}{12}.\]
\[\textbf{б)}\ Рисунок\ по\ условию\ задачи:\]
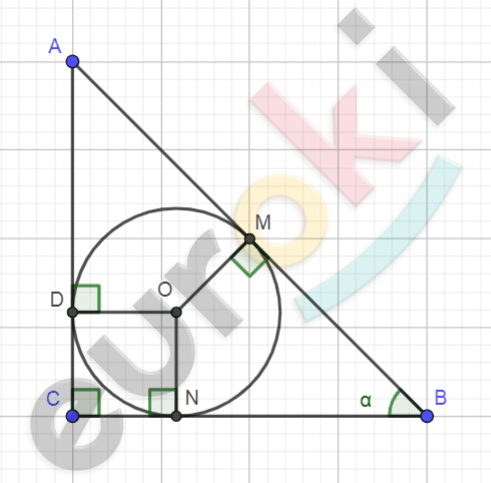
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - прямоугольный;\]
\[\angle C = 90{^\circ};\]
\[BC = a;\ \]
\[\angle B = \alpha.\]
\[\mathbf{Найти:}\]
\[S_{круга} - ?\]
\[\mathbf{Решение.}\]
\[1)\ OD = OM = ON = r;\]
\[2)\ Рассмотрим\ CNOD -\]
\[четырехугольник:\]
\[\angle C = \angle D = \angle N = 90{^\circ} \Longrightarrow\]
\[\Longrightarrow \ \angle O = 360{^\circ} - 90{^\circ} \bullet 4 = 90{^\circ}\ \]
\[(по\ теоремме\ у\ сумме\ углов).\]
\[DO = ON \Longrightarrow \ CDON - квадрат:\]
\[CN = ON = DO = CD = r.\]
\[3)\ tg\ \angle B = \frac{\text{AC}}{\text{BC}}\]
\[AC = BC \bullet tg\ \angle B = a\ \bullet tg\ \alpha.\]
\[4)\cos{\angle B} = \frac{\text{BC}}{\text{AB}}\]
\[AB = \frac{\text{BC}}{\cos{\angle B}} = \frac{a}{\cos\alpha}.\]
\[5)\ CD = AC - AD:\]
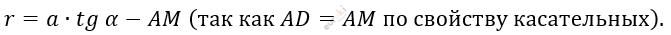
\[6)\ CN = CB - BN:\ \]
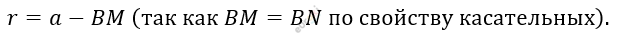
\[7)\ (r = a\ \bullet tg\ \alpha) + (r = a - BM)\]
\[2r = a \bullet tg\ \alpha + a - (AM + BM)\]
\[2r = a(tg\ \alpha + 1) - AB\]
\[2r = a(tg\ \alpha + 1) - \frac{a}{\cos\alpha} =\]
\[= a\left( \frac{\sin\alpha}{\cos\alpha} + 1 \right) - \frac{a}{\cos\alpha}\]
\[2r = \frac{a\left( \sin\alpha + \cos\alpha + 1 \right)}{\cos\alpha}\]
\[r = \frac{a}{2} \bullet \frac{\sin{\alpha + \cos\alpha} + 1}{\cos\alpha}\]
\[S = \pi r^{2} =\]
\[= \frac{\pi \bullet a^{2}\left( \sin\alpha + \cos\alpha - 1 \right)^{2}}{4 \bullet \cos^{2}\alpha}.\]
\[Ответ:S =\]
\[= \frac{\pi \bullet a^{2}\left( \sin\alpha + \cos\alpha - 1 \right)^{2}}{4 \bullet \cos^{2}\alpha}.\]
\[\mathbf{в)\ Рисунок\ по\ условию\ задачи:}\]
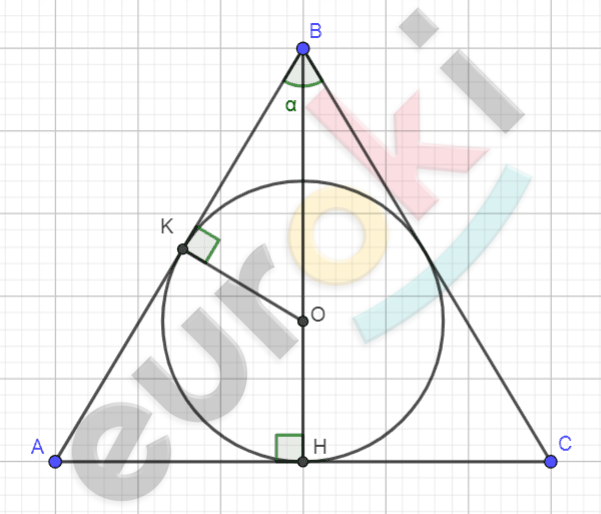
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равнобедренный;\]
\[AB = BC = a;\]
\[\angle B = \alpha.\]
\[\mathbf{Найти:}\]
\[S_{круга} - ?\]
\[\mathbf{Решение.}\]
\[1)\ OK = OH = r.\]
\[2)\ \angle ABH = \angle HBC = \frac{\alpha}{2}\ \]
\[(так\ как\ BH - бисектрисса).\]
\[3)\sin{\angle ABH} = \frac{\text{AH}}{\text{AB}}\]
\[AH = AB \bullet \sin\frac{\alpha}{2} = a \bullet \sin\frac{\alpha}{2}.\]
\[4)\cos{\angle ABH} = \frac{\text{BH}}{\text{AB}}\]
\[BH = AB \bullet \cos\frac{\alpha}{2} = a \bullet \cos\frac{\alpha}{2}.\]
\[5)\ \mathrm{\Delta}ABH\sim\mathrm{\Delta}KBO\ \]
\[(по\ двум\ углам):\]
\[\angle AHB = \angle BKO = 90{^\circ};\ \]
\[\angle ABH - общий.\]
\[Отсюда:\]
\[\frac{\text{AB}}{\text{BO}} = \frac{\text{AH}}{\text{OK}}.\]
\[6)\ BO = BH - OH = a \bullet \cos\frac{\alpha}{2} - r.\]
\[7)\ \frac{a}{a \bullet \cos\frac{\alpha}{2} - r} = \frac{a \bullet \sin\frac{\alpha}{2}}{r}\]
\[ar = a \bullet \sin\frac{\alpha}{2} \bullet \left( a \bullet \cos\frac{\alpha}{2} - r \right)\]
\[r = a \bullet \sin\frac{\alpha}{2} \bullet \cos\frac{\alpha}{2} - r \bullet \sin\frac{\alpha}{2}\]
\[r + r \bullet \sin\frac{\alpha}{2} = a \bullet \sin\frac{\alpha}{2} \bullet \cos\frac{\alpha}{2}\]
\[r\left( 1 + \sin\frac{\alpha}{2} \right) = \frac{a}{2} \bullet \sin\alpha\]
\[r = \frac{a \bullet \sin\alpha}{2\left( 1 + \sin\frac{\alpha}{2} \right)}.\]
\[8)\ S = \pi r^{2} = \frac{\pi \bullet a^{2} \bullet \sin^{2}\alpha}{4\left( 1 + \sin\frac{\alpha}{2} \right)^{2}}.\]
\[Ответ:S = \frac{\pi \bullet a^{2} \bullet \sin^{2}\alpha}{4\left( 1 + \sin\frac{\alpha}{2} \right)^{2}}.\]
\[\mathbf{г)\ Рисунок\ по\ условию\ задачи:}\]
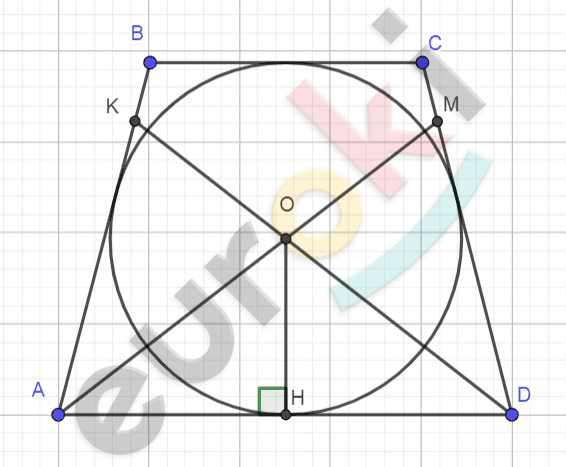
\[\mathbf{Дано:}\]
\[ABCD - равнобедренный\ \]
\[трапеция;\]
\[AB = CD;\ \]
\(AD = a\);
\[\angle A = \alpha.\]
\[\mathbf{Найти:}\]
\[S_{круга} - ?\]
\[\mathbf{Решение.}\]
\[1)\ ABCD - равнобедренная\ \]
\[трапеция:\]
\[\angle A = \angle D\ (по\ свойству).\]
\[2)\ AO\ и\ OD - биссектриссы:\]
\[\angle OAD = \angle ODA = \frac{\alpha}{2}.\]
\[3)\ \mathrm{\Delta}AOD - равнобедренный\ \]
\[(так\ как\ \angle OAD = \angle ODA):\]
\[AO = OD.\]
\[4)\ OH - является\ высотой,\ \]
\[медианой\ и\ биссектрисой:\]
\[AH = HD = \frac{\text{AD}}{2} = \frac{a}{2}.\]
\[5)\ \mathrm{\Delta}AOH - прямоугольный:\]
\[tg\ \angle OAH = \frac{\text{OH}}{\text{AH}}\]
\[OH = AH \bullet tg\ \angle OAH = \frac{a}{2} \bullet tg\frac{\alpha}{2}.\]
\[6)\ S = \pi r^{2} = \pi\left( \frac{a \bullet tg\frac{\alpha}{2}}{2} \right)^{2} =\]
\[= \frac{\pi \bullet a^{2} \bullet tg^{2}\frac{\alpha}{2}}{4}.\]
\[Ответ:S = \frac{\pi \bullet a^{2} \bullet tg^{2}\frac{\alpha}{2}}{4}.\]
\[\boxed{\mathbf{1117.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
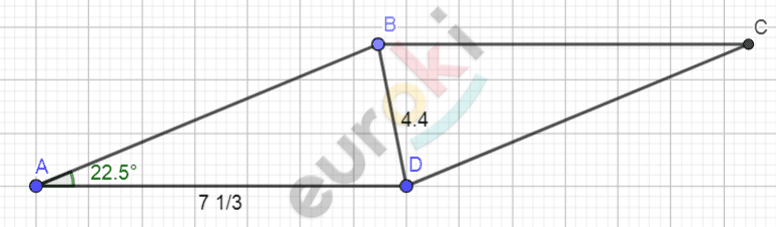
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм;\]
\[AD = 7\frac{1}{3}\ м;\]
\[BD = 4,4\ м;\]
\[\angle A = 22{^\circ}30^{'}.\]
\[\mathbf{Найти:}\]
\[\angle BD - ?\]
\[\angle DBC - ?\]
\[\mathbf{Решение.}\]
\[1)\ Рассмотрим\ \mathrm{\Delta}ABD.\]
\[По\ теореме\ синусов:\]
\[\frac{\text{BD}}{\sin{\angle A}} = \frac{\text{AD}}{\sin{\angle ABD}}\]
\[\sin{\angle ABD} \approx\]
\[\approx \left( 7\frac{1}{3} \bullet \sin{22{^\circ}30^{'}} \right)\ :4,4 =\]
\[= \left( 7\frac{1}{3} \bullet 0,38 \right)\ :4,4 =\]
\[= 0,6378;\ \ \ \angle ABD \approx 39{^\circ}38^{'}.\]
\[2)\ \angle ADB \approx\]
\[\approx 180{^\circ} - \left( 39{^\circ}38^{'} + 22{^\circ}30^{'} \right) \approx\]
\[\approx 117{^\circ}52^{'}.\]
\[3)\ \angle ABD = \angle BDC = 39{^\circ}38^{'}.\]
\[\angle ADB = \angle DBC =\]
\[= 117{^\circ}52^{'}\ (как\ накрестлежащие).\]
\[Ответ:\angle BDC = 39{^\circ}38^{'};\ \]
\[\angle DBC = 117{^\circ}52'.\]
