Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 1278
Задание 1278
\[\boxed{\mathbf{1278.ОК\ ГДЗ - домашка\ н}а\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
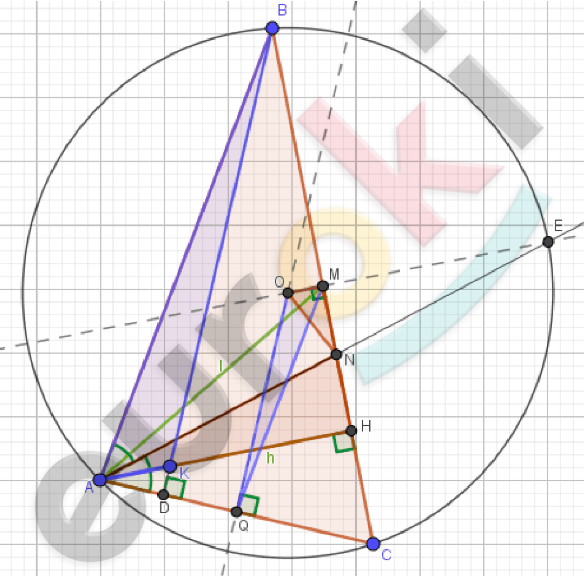
\[Дано:\ \]
\[\mathrm{\Delta}ABC;\]
\[AH - высота;\ \]
\[AM - медиана;\ \]
\[\text{AN} - биссектриса;\]
\[AH = h;\]
\[AM = l;\ \]
\[MN = NH;\ \]
\[BD - высота;\ \]
\[K = AH \cap BD.\]
\[Найти:\]
\[AK - ?\]
\[Решение.\]
\[1)\ По\ теореме\ Пифагора\ из\ \]
\[\mathrm{\Delta}MAH:\]
\[MH^{2} = l^{2} - h^{2}\]
\[MN = NH = \frac{1}{2}MH = \frac{\sqrt{t^{2} - h^{2}}}{2}.\]
\[2)\ Проведем\ два\ серединных\ \]
\[перпендикуляра:\]
\[QO\bot AC;\ AQ = AC;\ MO\bot BC;\ \ \]
\[O = QO \cap MO.\]
\[На\ их\ пересечении\ построим\ \]
\[описанную\ окружность\ O(O,\ R).\]
\[Отметим\ точку\ E\ пересечения\ \]
\[биссектрисы\ и\ серединного\]
\[перпендикуляра\ на\ \]
\[окружность:\ \ E = OM \cap A.\]
\[MQ - средняя\ линия\ \mathrm{\Delta}ABC \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} MQ = \frac{18}{2}\text{AB} \\ MQ||AB\ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ .\]
\[3)\ В\ \mathrm{\Delta}MOQ\ и\ \mathrm{\Delta}AKB\ углы\ \]
\[образованы\ параллельными\ \]
\[прямыми.\]
\[\mathrm{\Delta}MOQ\sim\mathrm{\Delta}AKB - по\ двум\ углам:\]
\[\left. \ \begin{matrix} \angle MOQ = \angle AKB \\ \angle OMQ = \angle KAB \\ \end{matrix} \right\}.\]
\[4)\ k = \frac{\text{AB}}{\text{MQ}} = 2 \Longrightarrow AK = 2MO.\]
\[\mathrm{\Delta}ANH = \mathrm{\Delta}ENM - по\ второму\ \]
\[признаку:\]
\[NH = NM;\]
\[\angle AHN = \angle EMN = 90{^\circ};\]
\[\angle ANH = \angle ENM -\]
\[вертикальные.\]
\[Отсюда:\]
\[AN = EN.\]
\[5)\ \mathrm{\Delta}AOE - равнобедренный:\]
\[\left\{ \begin{matrix} OA = OE = R \\ AN = EN\ \ \ \ \ \ \ \ \ \\ \end{matrix}\ \right.\ \]
\[ON - медиана,\ биссектриса,\]
\[высота;\]
\[\angle ONM = \angle NAH - образованы\ \]
\[двумя\ парами\ \]
\[взаимноперпендикулярных\ \]
\[сторон.\]
\[\mathrm{\Delta}ONM\sim\mathrm{\Delta}NAH - по\ двум\ углам:\]
\[\angle ONM = \angle NAH;\]
\[\angle OMN = \angle NHA = 90{^\circ}.\]
\[Отсюда:\]
\[\frac{\text{MN}}{\text{AN}} = \frac{\text{OM}}{\text{NH}}\]
\[OM = \frac{MN \cdot NH}{\text{AN}} =\]
\[= \frac{\frac{\sqrt{l^{2} - h^{2}}}{2} \cdot \frac{\sqrt{l^{2} - h^{2}}}{2}}{h} = \frac{l^{2} - h^{2}}{4h}.\]
\[AK = 2MO = \frac{l^{2} - h^{2}}{2h}.\]
\[Ответ:\ AK = \frac{l^{2} - h^{2}}{2h}.\]
