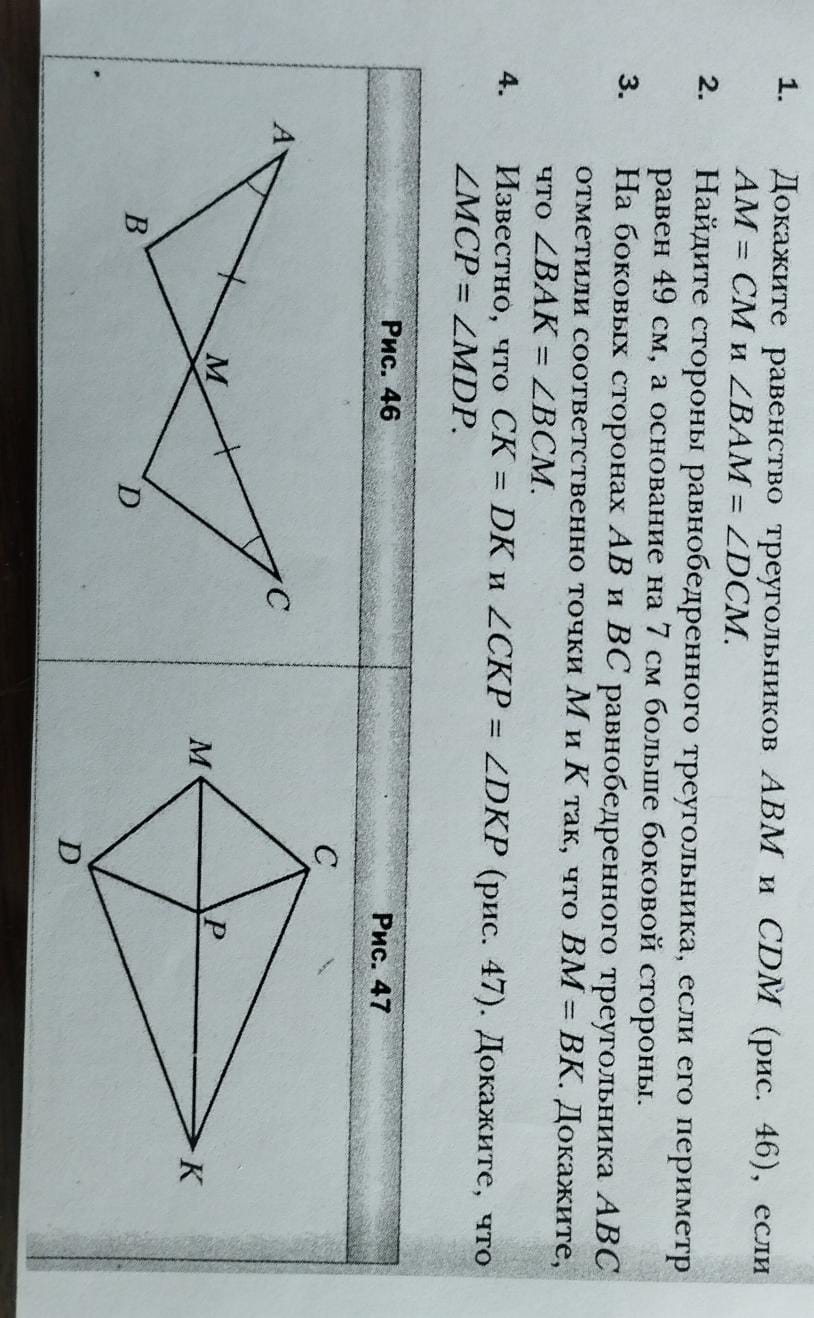
1. Докажите равенство треугольников АВМ и CDM (рис. 46), если AM = CM и ∠BAM = ∠DCM.

Для доказательства равенства треугольников АВМ и CDM мы можем использовать признак равенства треугольников по двум сторонам и углу между ними (СУС). У нас дано, что AM = CM (по условию). Также, углы ∠BAM и ∠DCM равны (по условию). Стороны AB и CD являются сторонами треугольников АВМ и CDM. Однако из условия не следует, что стороны AB = CD. И стороны BM и MD также не являются данными по условию. Заметим, что углы ∠AMB и ∠CMD являются вертикальными, а значит, они равны. Следовательно, треугольники АВМ и CDM равны по первому признаку равенства треугольников (по стороне и двум прилежащим углам), т.е., если сторона и два угла одного треугольника равны соответственно стороне и двум углам другого треугольника. Таким образом: 1. AM = CM (по условию) 2. ∠BAM = ∠DCM (по условию) 3. ∠AMB = ∠CMD (как вертикальные углы) Следовательно, треугольники АВМ и CDM равны по первому признаку равенства треугольников (по стороне AM=CM и прилегающим к ней углам).