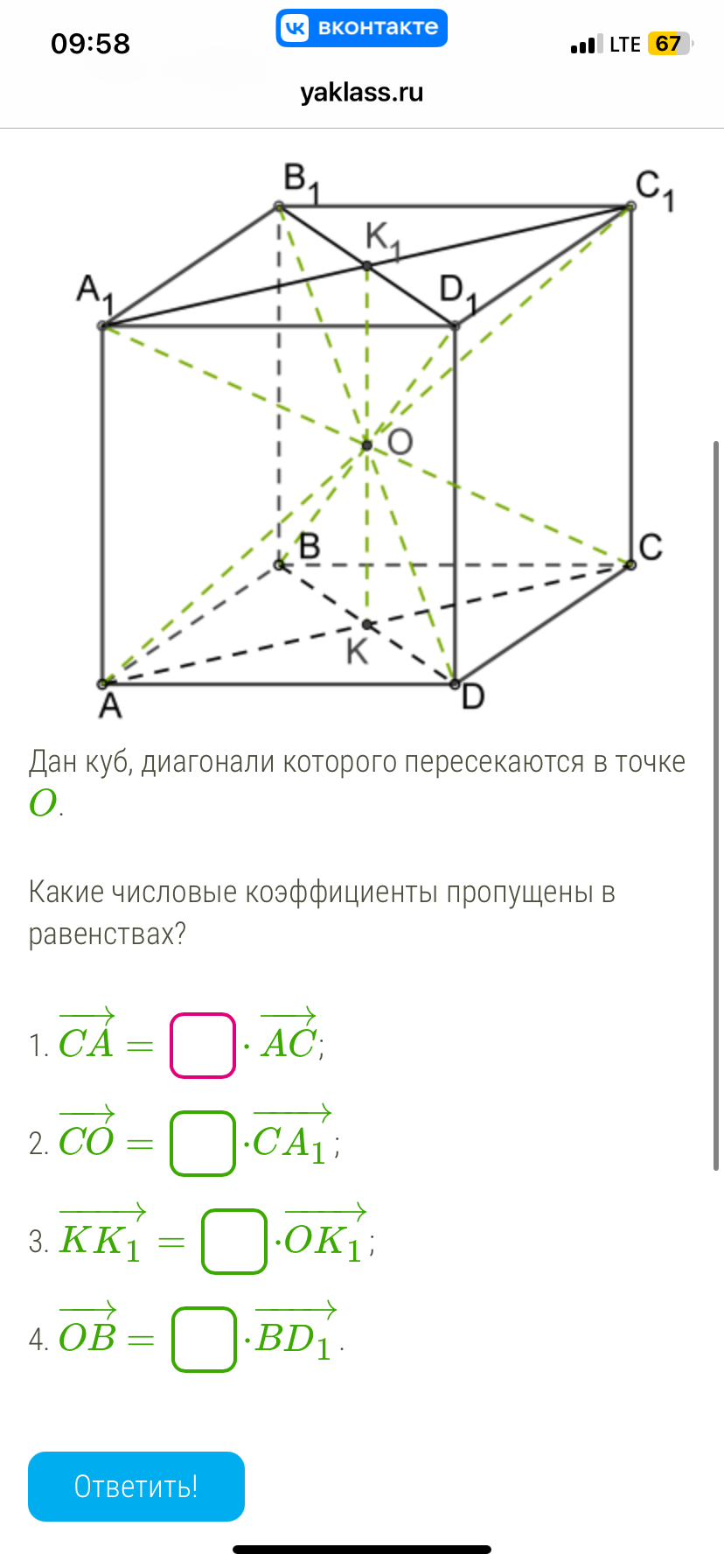
Дан куб, диагонали которого пересекаются в точке O. Какие числовые коэффициенты пропущены в равенствах? 1. $$\vec{CA} = \boxed{?} \cdot \vec{AC}$$; 2. $$\vec{CO} = \boxed{?} \cdot \vec{CA_1}$$; 3. $$\vec{KK_1} = \boxed{?} \cdot \vec{OK_1}$$; 4. $$\vec{OB} = \boxed{?} \cdot \vec{BD_1}$$.

Рассмотрим каждое равенство по порядку:

1. Вектор $$\vec{CA}$$ противоположен по направлению вектору $$\vec{AC}$$ и имеет ту же длину. Следовательно, $$\vec{CA} = -1 \cdot \vec{AC}$$.

2. Точка $$O$$ является серединой диагонали $$CA_1$$, поэтому вектор $$\vec{CO}$$ равен половине вектора $$\vec{CA_1}$$. Следовательно, $$\vec{CO} = \frac{1}{2} \cdot \vec{CA_1}$$.

3. В кубе $$KK_1$$ - это ребро, а $$OK_1$$ половина диагонали грани. Так как куб, то $$KK_1 = OK_1$$. Так как вектора сонаправлены, то $$\vec{KK_1} = 1 \cdot \vec{OK_1}$$.

4. Точка $$O$$ является серединой диагонали $$BD_1$$, поэтому вектор $$\vec{OB}$$ равен половине вектора $$\vec{BD_1}$$. Следовательно, $$\vec{OB} = \frac{1}{2} \cdot \vec{BD_1}$$.

Таким образом, пропущенные коэффициенты:

1. -1
2. 1/2
3. 1
4. 1/2