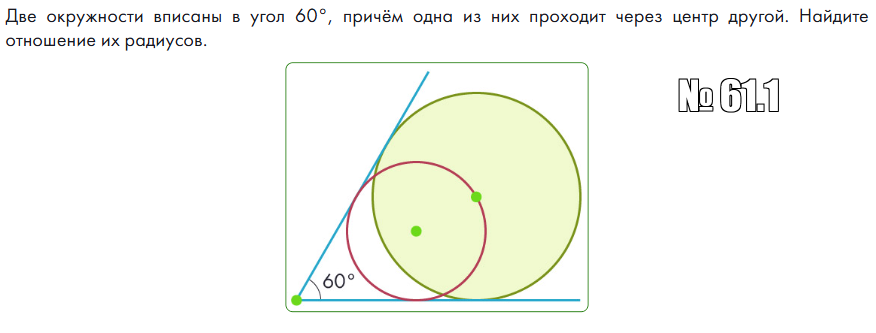
Две окружности вписаны в угол 60°, причём одна из них проходит через центр другой. Найдите отношение их радиусов.

Представим решение задачи по шагам: 1. Обозначения и построения: * Пусть $$O_1$$ – центр меньшей окружности, $$r$$ – её радиус. * Пусть $$O_2$$ – центр большей окружности, $$R$$ – её радиус. * По условию, меньшая окружность проходит через центр большей, значит, $$O_1O_2 = r$$. * Обозначим вершину угла как $$A$$. * $$O_1$$ и $$O_2$$ лежат на биссектрисе угла $$A$$. * Расстояние от $$O_1$$ до стороны угла равно $$r$$, а от $$O_2$$ до стороны угла равно $$R$$. 2. Рассмотрим прямоугольные треугольники: * Проведем перпендикуляры из $$O_1$$ и $$O_2$$ на одну из сторон угла $$A$$. Получим прямоугольные треугольники $$\triangle AO_1H_1$$ и $$\triangle AO_2H_2$$, где $$H_1$$ и $$H_2$$ – основания перпендикуляров. * Углы $$\angle O_1AH_1$$ и $$\angle O_2AH_2$$ равны 30°, так как $$AO_1$$ и $$AO_2$$ – биссектрисы угла в 60°. 3. Выразим расстояния от вершины угла до центров окружностей: * В $$\triangle AO_1H_1$$: $$\sin 30^\circ = \frac{O_1H_1}{AO_1} = \frac{r}{AO_1}$$. Так как $$\sin 30^\circ = \frac{1}{2}$$, то $$AO_1 = 2r$$. * В $$\triangle AO_2H_2$$: $$\sin 30^\circ = \frac{O_2H_2}{AO_2} = \frac{R}{AO_2}$$. Так как $$\sin 30^\circ = \frac{1}{2}$$, то $$AO_2 = 2R$$. 4. Соотношение между расстояниями: * Так как точки $$A$$, $$O_1$$ и $$O_2$$ лежат на одной прямой, то $$AO_2 = AO_1 + O_1O_2$$. * Подставляем известные значения: $$2R = 2r + r$$, откуда $$2R = 3r$$. 5. Найдем отношение радиусов: * Из уравнения $$2R = 3r$$ получаем $$\frac{R}{r} = \frac{3}{2}$$. Ответ: 3/2