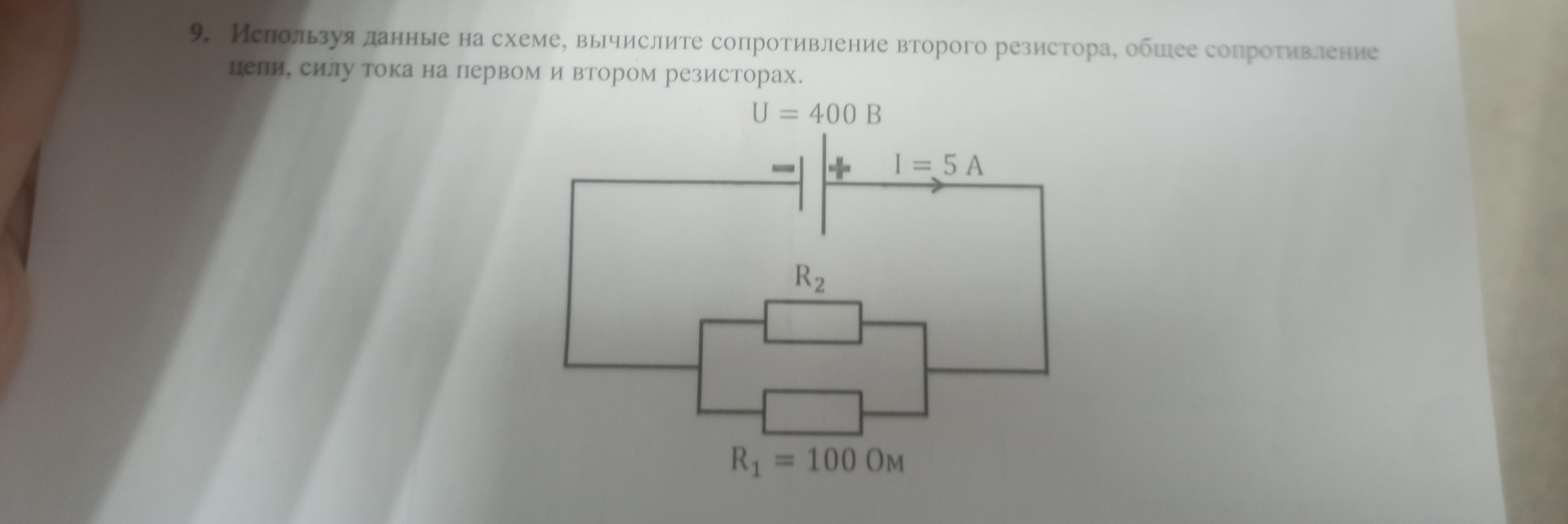
Вопрос:
Используя данные на схеме, вычислите сопротивление второго резистора, общее сопротивление цепи, силу тока на первом и втором резисторах.
Ответ:
Здравствуйте, ребята! Давайте решим эту задачу вместе, шаг за шагом.
1. Анализ схемы и известных данных
Нам дана следующая информация:
* Напряжение источника питания: (U = 400 , ext{В})
* Общий ток в цепи: (I = 5 , ext{А})
* Сопротивление первого резистора: (R_1 = 100 , ext{Ом})
Нам нужно найти:
* Сопротивление второго резистора: (R_2)
* Общее сопротивление цепи: (R_{ ext{общ}})
* Ток через первый резистор: (I_1)
* Ток через второй резистор: (I_2)
2. Расчет общего сопротивления цепи
По закону Ома, общее сопротивление цепи можно найти как:
\[R_{\text{общ}} = \frac{U}{I} = \frac{400 , \text{В}}{5 , \text{А}} = 80 , \text{Ом}\]
3. Расчет сопротивления второго резистора
Так как резисторы (R_1) и (R_2) соединены параллельно, их общее сопротивление вычисляется по формуле:
\[\frac{1}{R_{\text{общ}}} = \frac{1}{R_1} + \frac{1}{R_2}\]
Подставим известные значения:
\[\frac{1}{80} = \frac{1}{100} + \frac{1}{R_2}\]
Выразим (\frac{1}{R_2}):
\[\frac{1}{R_2} = \frac{1}{80} - \frac{1}{100} = \frac{5 - 4}{400} = \frac{1}{400}\]
Отсюда:
\[R_2 = 400 , \text{Ом}\]
4. Расчет тока через первый резистор
По закону Ома для первого резистора:
\[I_1 = \frac{U}{R_1} = \frac{400 , \text{В}}{100 , \text{Ом}} = 4 , \text{А}\]
5. Расчет тока через второй резистор
По закону Ома для второго резистора:
\[I_2 = \frac{U}{R_2} = \frac{400 , \text{В}}{400 , \text{Ом}} = 1 , \text{А}\]
6. Проверка
Убедимся, что сумма токов через оба резистора равна общему току в цепи:
\[I = I_1 + I_2 = 4 , \text{А} + 1 , \text{А} = 5 , \text{А}\]
Это соответствует известному значению общего тока.
Ответ:
* Сопротивление второго резистора: (R_2 = 400 , \text{Ом})
* Общее сопротивление цепи: (R_{\text{общ}} = 80 , \text{Ом})
* Ток через первый резистор: (I_1 = 4 , \text{А})
* Ток через второй резистор: (I_2 = 1 , \text{А})
Надеюсь, это решение было полезным и понятным для вас!