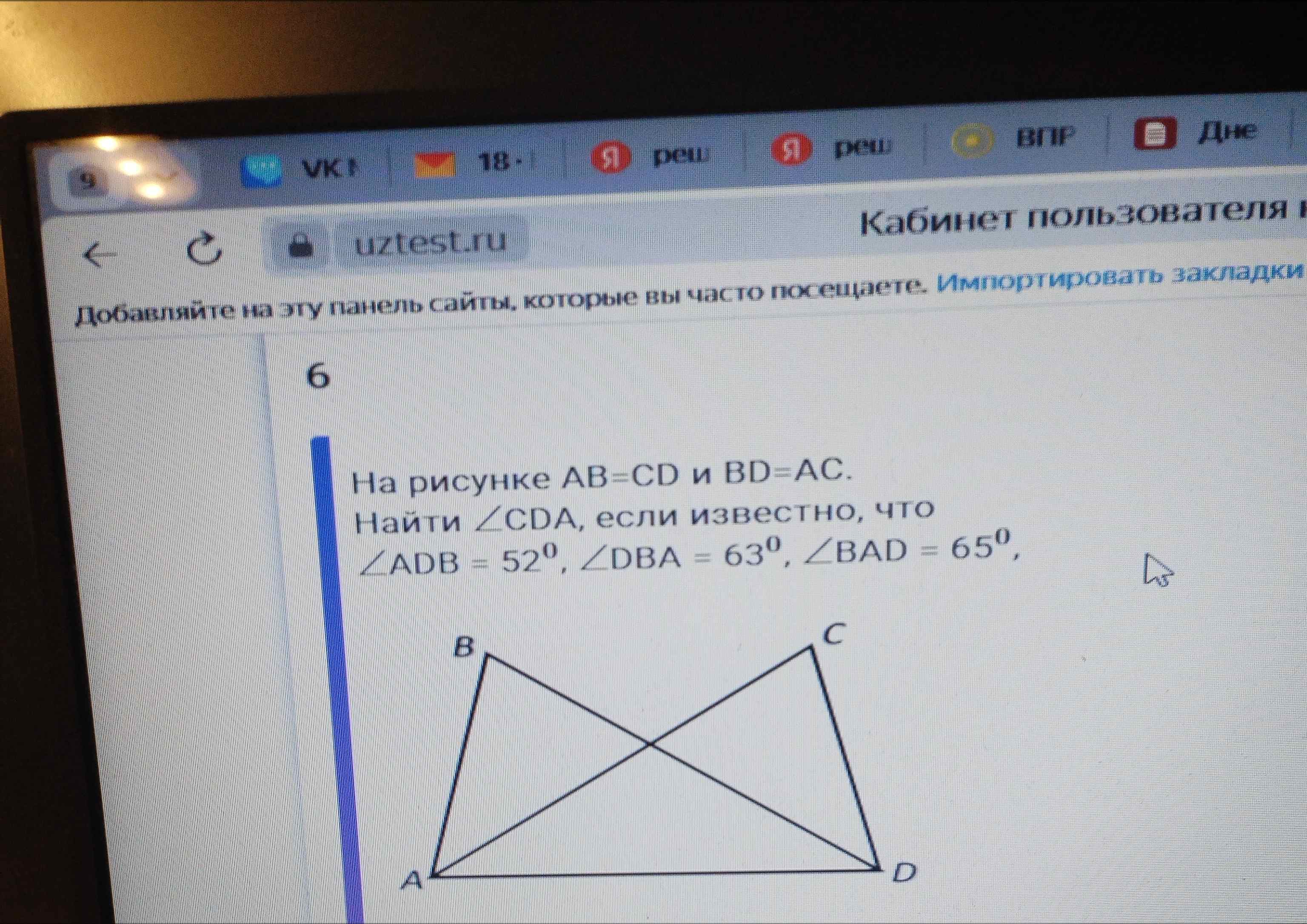
На рисунке AB=CD и BD=AC. Найти ∠CDA, если известно, что ∠ADB = 52°, ∠DBA = 63°, ∠BAD = 65°.

Для решения данной задачи необходимо рассмотреть треугольники ABD и DBC.

Шаг 1: Рассмотрим треугольник ABD.

Нам известны углы ∠ADB = 52° и ∠DBA = 63°. Найдем угол ∠BAD.

Сумма углов в треугольнике равна 180°. Следовательно:

$$∠BAD = 180° - ∠ADB - ∠DBA = 180° - 52° - 63° = 65°$$

Шаг 2: Рассмотрим треугольники ABD и CDB.

По условию AB = CD и BD = AC, но необходимо доказать равенство треугольников ABD и CDB, у которых AB = CD, BD = AC, AD - общая сторона. Треугольники ABD и CDB не равны. Равенство углов ∠BAD = 65° дано в условии, но эта информация избыточна и может запутать.

Заметим, что треугольники ABD и BCD равны по трем сторонам (AB=CD, BD=AC, AD - общая сторона), но это не может быть из условия, так как AC и BD - диагонали четырехугольника, а не стороны треугольника BCD.

Ошибка в условии. Должно быть: На рисунке AB=CD и AD=BC. Найти ∠CDA, если известно, что ∠ADB = 52°, ∠DBA = 63°, ∠BAD = 65°.

Тогда:

Шаг 1: Рассмотрим треугольники ABD и CDB.

Мы знаем, что AB = CD и AD = BC. Сторона BD - общая.

Следовательно, треугольники ABD и CDB равны по трем сторонам (AB = CD, AD = BC, BD - общая).

Шаг 2: Найдем соответствующие углы.

Так как треугольники ABD и CDB равны, то ∠ADB = ∠CBD = 52° и ∠ABD = ∠CDB.

Шаг 3: Найдем угол ∠ABD.

В треугольнике ABD мы знаем ∠ADB = 52° и ∠BAD = 65°.

Тогда, ∠ABD = 180° - 52° - 65° = 63°.

Шаг 4: Найдем угол ∠CDB.

Так как ∠ABD = ∠CDB, то ∠CDB = 63°.

Шаг 5: Найдем угол ∠CDA.

∠CDA = ∠CDB + ∠BDA = 63° + 52° = 115°.

Ответ: 115°