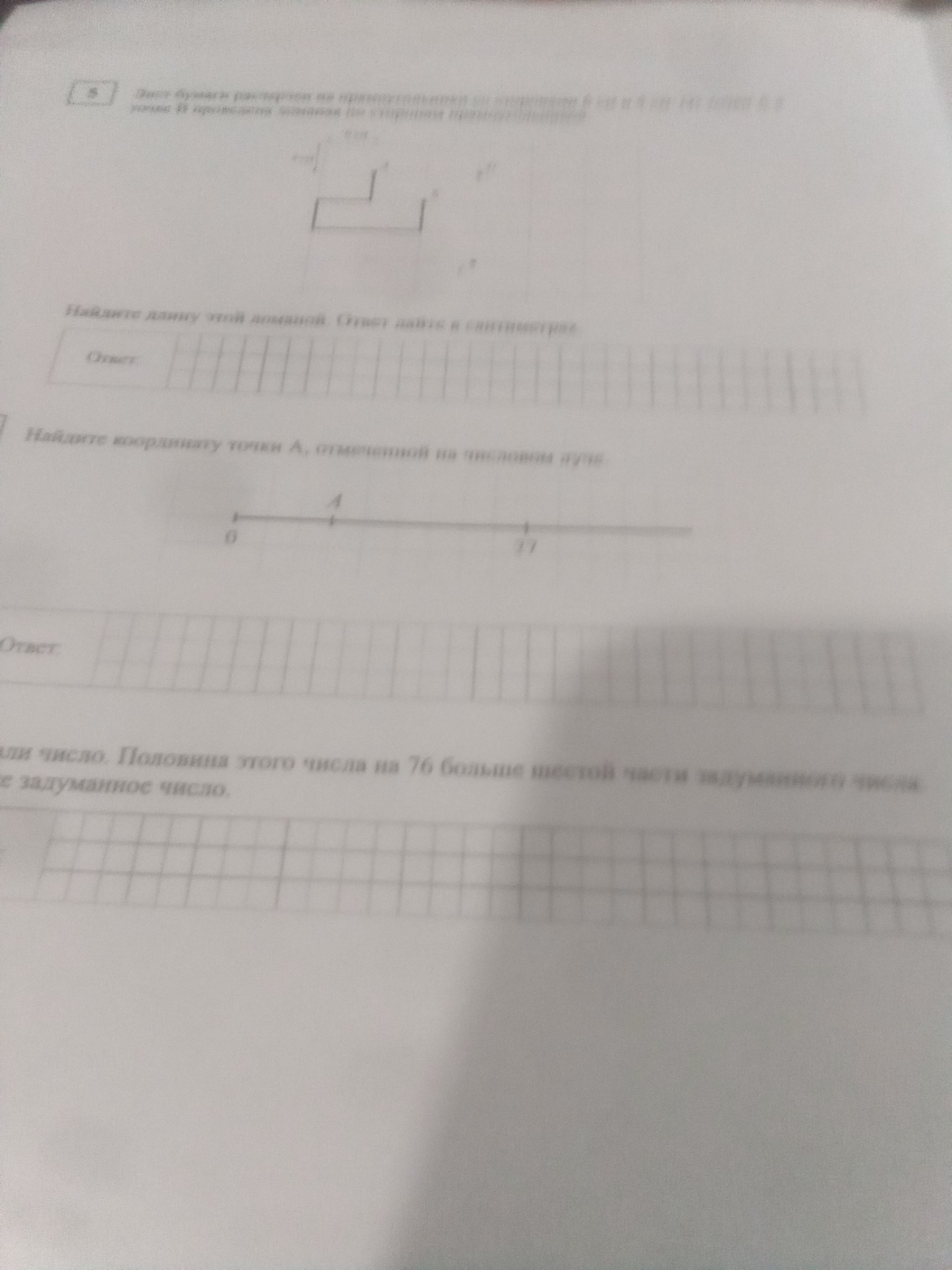
Найдите длину этой ломаной. Ответ дайте в сантиметрах. (Первая ломаная: 6, 4, 6, 4, 6. Вторая задача: Найдите координату точки A, отмеченной на числовом луче, если отрезок от 0 до 27 разбит на 3 равные части. Третья задача: Задумали число. Половина этого числа на 76 больше шестой части задуманного числа.)

Задача 1: Найдите длину ломаной. Длина ломаной равна сумме длин её отрезков. На рисунке изображена ломаная, состоящая из пяти отрезков, длины которых равны 6 см, 4 см, 6 см, 4 см и 6 см. Следовательно, длина ломаной равна: 6 + 4 + 6 + 4 + 6 = 26 см Ответ: 26 Задача 2: Найдите координату точки A. На числовом луче отмечены точки 0 и 27. Отрезок между 0 и 27 разделен на 3 равные части. Точка A находится на первой отметке после 0. Чтобы найти координату точки A, нужно разделить 27 на 3. $\frac{27}{3} = 9$ Ответ: 9 Задача 3: Задумали число. Половина этого числа на 76 больше шестой части задуманного числа. Пусть x - задуманное число. Тогда половина этого числа - $\frac{x}{2}$, а шестая часть - $\frac{x}{6}$. По условию, половина числа на 76 больше шестой части, поэтому мы можем записать уравнение: $\frac{x}{2} = \frac{x}{6} + 76$ Для решения этого уравнения, умножим обе части на 6, чтобы избавиться от дробей: $6 \cdot \frac{x}{2} = 6 \cdot (\frac{x}{6} + 76)$ $3x = x + 456$ Теперь вычтем x из обеих частей уравнения: $3x - x = 456$ $2x = 456$ Разделим обе части на 2, чтобы найти x: $x = \frac{456}{2}$ $x = 228$ Ответ: 228