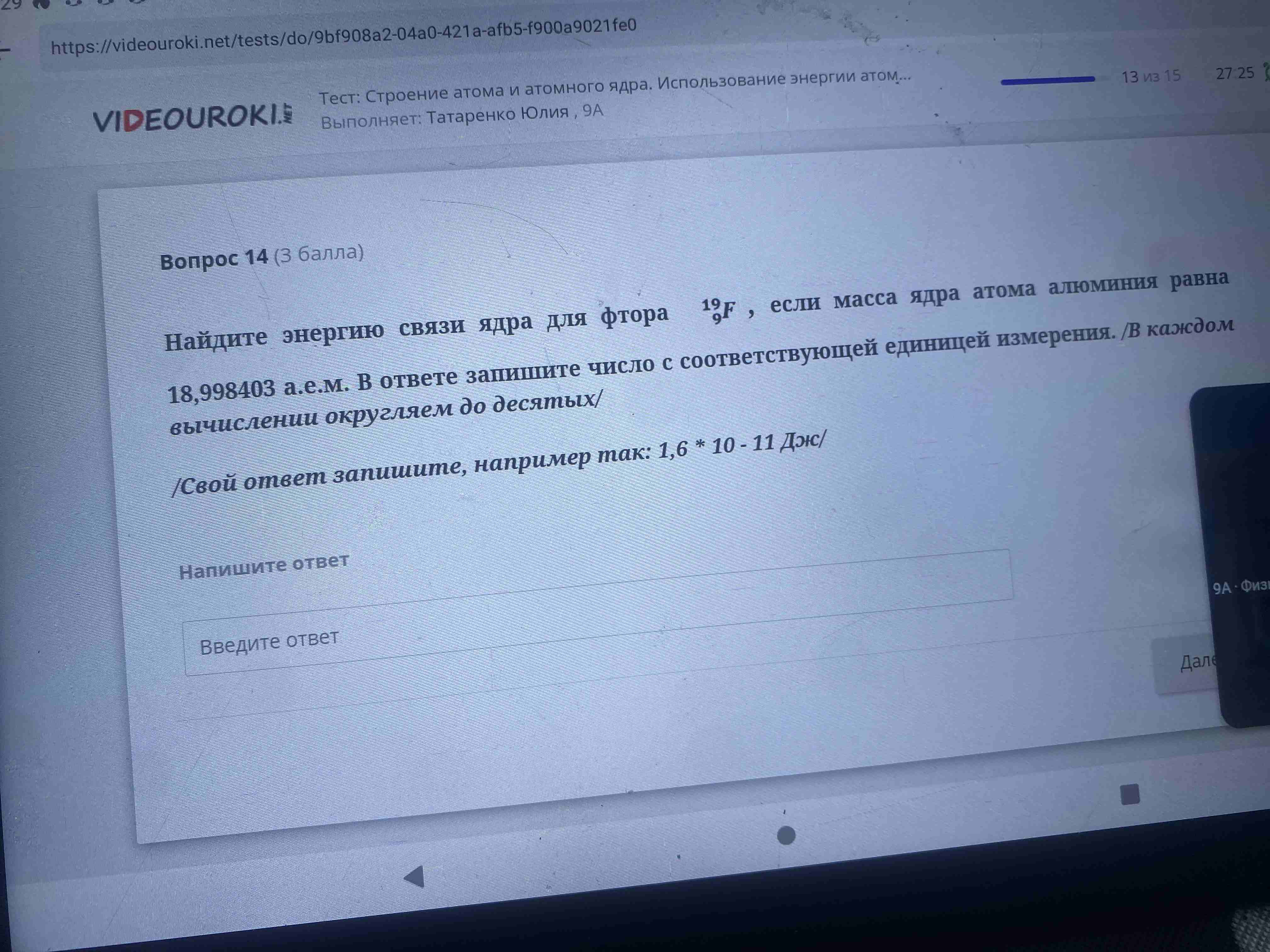
Найдите энергию связи ядра для фтора $$^{19}_9F$$, если масса ядра атома фтора равна 18,998403 а.е.м. В ответе запишите число с соответствующей единицей измерения. /В каждом вычислении округляем до десятых/

Для расчета энергии связи ядра фтора $$^{19}_9F$$, нам понадобятся следующие данные: 1. Масса протона ($$m_p$$) = 1,00728 а.е.м. 2. Масса нейтрона ($$m_n$$) = 1,00866 а.е.м. 3. Масса ядра фтора ($$m_ядра$$) = 18,998403 а.е.м. Ядро фтора содержит 9 протонов и 10 нейтронов (19 - 9 = 10). 1. Рассчитаем дефект массы ($$\Delta m$$): $$\Delta m = (9 \cdot m_p + 10 \cdot m_n) - m_ядра$$ $$\Delta m = (9 \cdot 1,00728 + 10 \cdot 1,00866) - 18,998403$$ $$\Delta m = (9,06552 + 10,0866) - 18,998403$$ $$\Delta m = 19,15212 - 18,998403$$ $$\Delta m = 0,153717$$ а.е.м. 2. Переведем дефект массы в энергию (энергия связи) с использованием формулы Эйнштейна $$E = \Delta m \cdot c^2$$: Энергию удобно выразить в МэВ. 1 а.е.м. соответствует 931,5 МэВ. $$E = 0,153717 \cdot 931,5$$ $$E = 143,18$$ МэВ 3. Переведем энергию в Джоули (Дж): 1 МэВ = 1,602 * 10⁻¹³ Дж $$E = 143,18 \cdot 1,602 \cdot 10^{-13}$$ $$E = 229,37 \cdot 10^{-13}$$ Дж $$E = 2,2937 \cdot 10^{-11}$$ Дж Округлим до десятых: $$E \approx 2,3 \cdot 10^{-11}$$ Дж Ответ: 2,3 * 10^-11 Дж