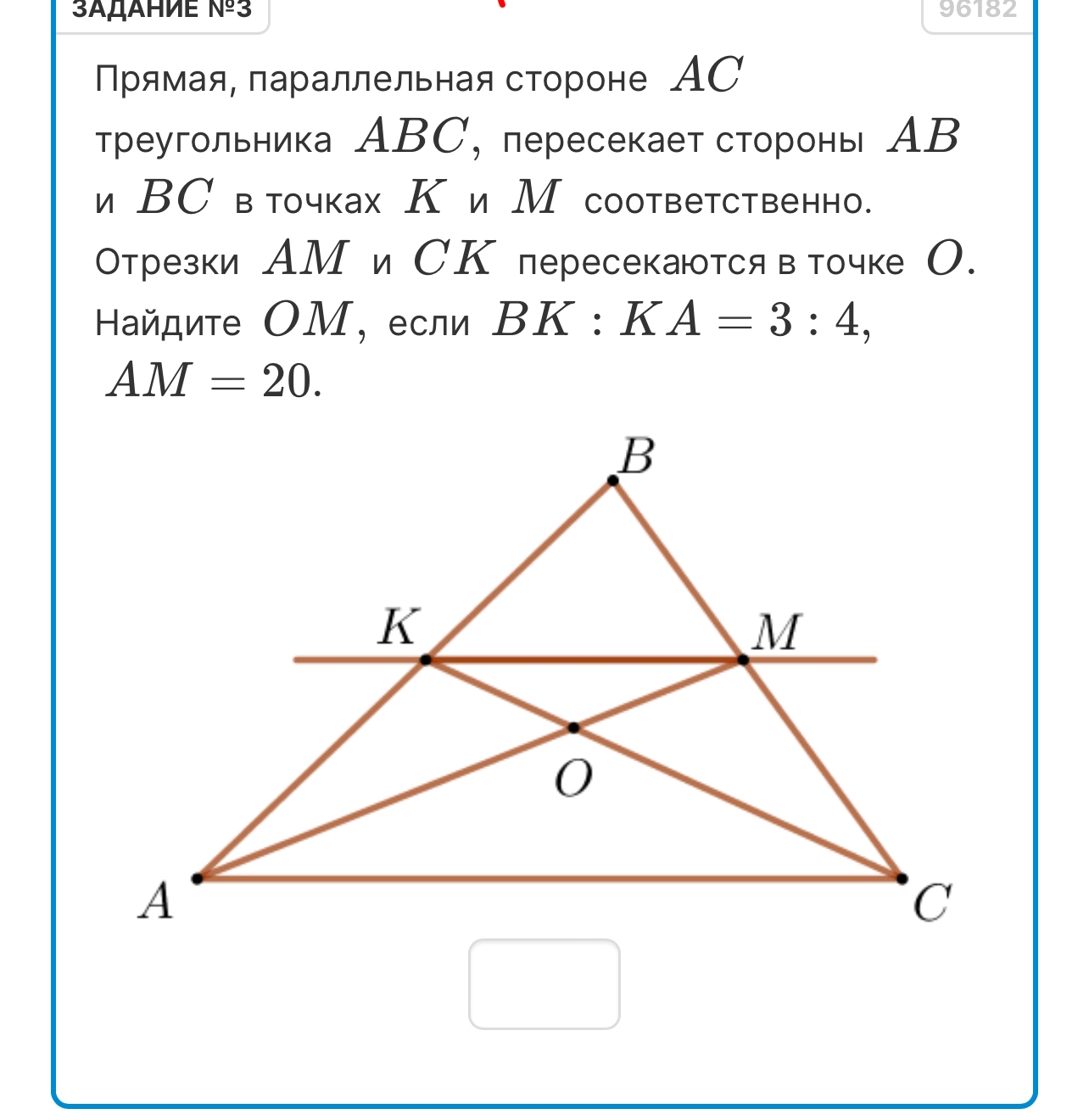
Найдите OM, если BK:KA = 3:4, AM = 20. Прямая KM параллельна AC.

Давайте разберем решение этой задачи по геометрии. 1. **Анализ условия:** - У нас есть треугольник ABC. - Прямая KM параллельна стороне AC. - Точки K и M лежат на сторонах AB и BC соответственно. - Отрезки AM и CK пересекаются в точке O. - BK:KA = 3:4 - AM = 20 - Наша задача – найти длину отрезка OM. 2. **Применим теорему Менелая:** Для треугольника ABM и секущей CK мы можем применить теорему Менелая. Теорема Менелая гласит: $$\frac{AK}{KB} \cdot \frac{BC}{CM} \cdot \frac{MO}{OA} = 1$$ Используем известные отношения, \(\frac{AK}{KB} = \frac{4}{3}\). 3. **Используем подобие треугольников:** Поскольку KM параллельна AC, то треугольники BKM и BAC подобны. Значит, \(\frac{BK}{BA} = \frac{BM}{BC}\). Из условия \(BK:KA = 3:4\), следует \(BK:BA = 3:(3+4) = 3:7\). Значит, \(\frac{BM}{BC} = \frac{3}{7}\). Следовательно, \(\frac{MC}{BC} = 1 - \frac{3}{7} = \frac{4}{7}\). Значит, \(\frac{BC}{MC} = \frac{7}{4}\). 4. **Подстановка в теорему Менелая:** Подставим известные значения в теорему Менелая: $$\frac{4}{3} \cdot \frac{7}{4} \cdot \frac{MO}{OA} = 1$$ 5. **Вычисляем отношение MO/OA:** Упрощаем уравнение: $$\frac{7}{3} \cdot \frac{MO}{OA} = 1$$ $$\frac{MO}{OA} = \frac{3}{7}$$ Пусть MO = 3x, тогда OA = 7x. Следовательно AM = MO + OA = 3x + 7x = 10x. 6. **Находим x:** Из условия AM = 20, поэтому: $$10x = 20$$ $$x = 2$$ 7. **Находим OM:** Теперь найдем OM: $$OM = 3x = 3 \cdot 2 = 6$$ **Ответ:** Длина отрезка OM равна 6.