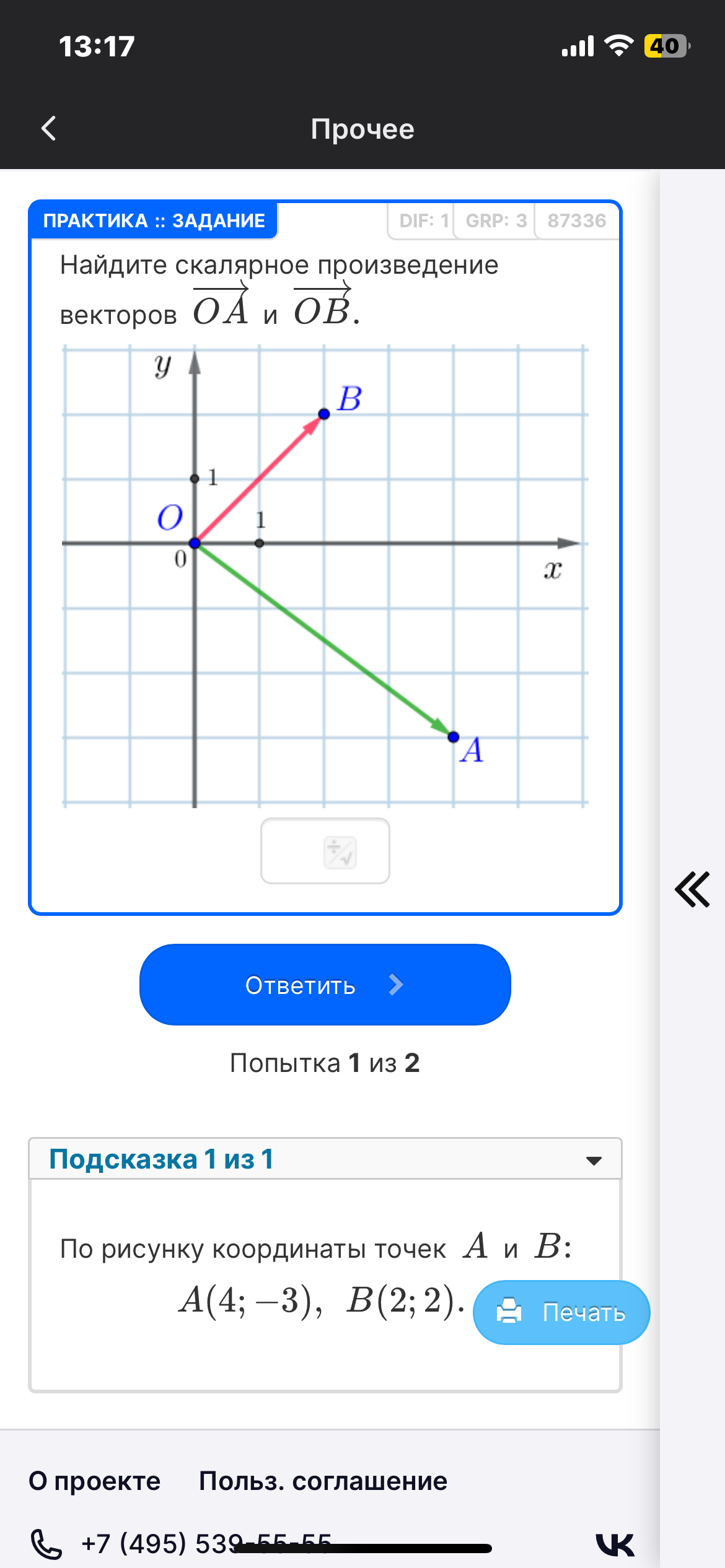
Вопрос:
Найдите скалярное произведение векторов \(\vec{OA}\) и \(\vec{OB}\), если известны координаты точек \(A(4; -3)\) и \(B(2; 2)\).
Ответ:
Для решения задачи нужно найти скалярное произведение векторов \(\vec{OA}\) и \(\vec{OB}\). Из условия известны координаты точек \(A(4; -3)\) и \(B(2; 2)\). Координаты точки \(O\) (начало координат) равны \((0; 0)\).
1. Найдем координаты вектора \(\vec{OA}\):
\(\vec{OA} = A - O = (4 - 0; -3 - 0) = (4; -3)\)
2. Найдем координаты вектора \(\vec{OB}\):
\(\vec{OB} = B - O = (2 - 0; 2 - 0) = (2; 2)\)
3. Найдем скалярное произведение векторов \(\vec{OA}\) и \(\vec{OB}\). Скалярное произведение двух векторов \(\vec{a} = (x_1; y_1)\) и \(\vec{b} = (x_2; y_2)\) вычисляется по формуле:
\(\vec{a} \cdot \vec{b} = x_1 \cdot x_2 + y_1 \cdot y_2\)
В нашем случае:
\(\vec{OA} \cdot \vec{OB} = (4 \cdot 2) + (-3 \cdot 2) = 8 - 6 = 2\)
Таким образом, скалярное произведение векторов \(\vec{OA}\) и \(\vec{OB}\) равно 2.
Ответ: 2
Развёрнутый ответ для школьника:
Привет! Давай решим эту задачу вместе. Нам нужно найти скалярное произведение двух векторов, \(\vec{OA}\) и \(\vec{OB}\). Координаты точек \(A\) и \(B\) нам известны, а точка \(O\) - это начало координат (то есть точка \((0; 0)\)).
Сначала определим координаты векторов \(\vec{OA}\) и \(\vec{OB}\). Так как точка \(O\) – это начало координат, координаты векторов будут просто координатами точек \(A\) и \(B\):
* Вектор \(\vec{OA}\) имеет координаты \((4; -3)\).
* Вектор \(\vec{OB}\) имеет координаты \((2; 2)\).
Теперь, чтобы найти скалярное произведение, нужно перемножить соответствующие координаты и сложить результаты:
\(\vec{OA} \cdot \vec{OB} = (4 \cdot 2) + (-3 \cdot 2) = 8 - 6 = 2\)
Вот и всё! Скалярное произведение векторов \(\vec{OA}\) и \(\vec{OB}\) равно 2.