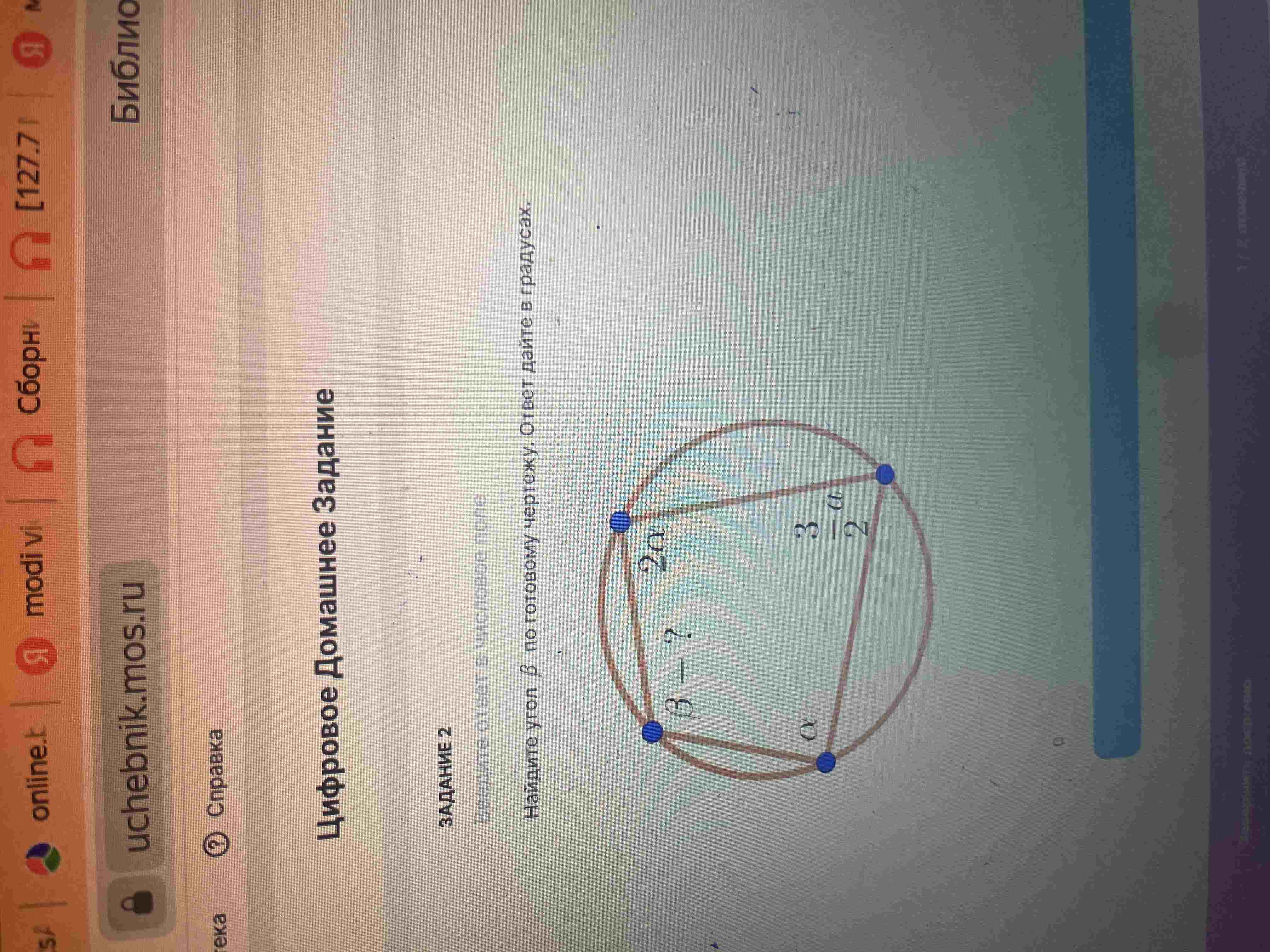
Вопрос:
Найдите угол \(\beta\) по готовому чертежу. Ответ дайте в градусах.
Ответ:
Для решения этой задачи воспользуемся свойством вписанного четырехугольника. Сумма противоположных углов вписанного четырехугольника равна 180 градусам.
В данном случае у нас есть вписанный четырехугольник, углы которого равны \(\alpha\), \(\beta\), \(2\alpha\), и \(\frac{3}{2}\alpha\).
Таким образом, можем записать два уравнения:
1) \(\alpha + 2\alpha = 180^{\circ}\)
2) \(\beta + \frac{3}{2}\alpha = 180^{\circ}\)
Решим первое уравнение:
\(3\alpha = 180^{\circ}\)
\(\alpha = \frac{180^{\circ}}{3}\)
\(\alpha = 60^{\circ}\)
Теперь подставим значение \(\alpha\) во второе уравнение:
\(\beta + \frac{3}{2} \cdot 60^{\circ} = 180^{\circ}\)
\(\beta + 90^{\circ} = 180^{\circ}\)
\(\beta = 180^{\circ} - 90^{\circ}\)
\(\beta = 90^{\circ}\)
Ответ: 90