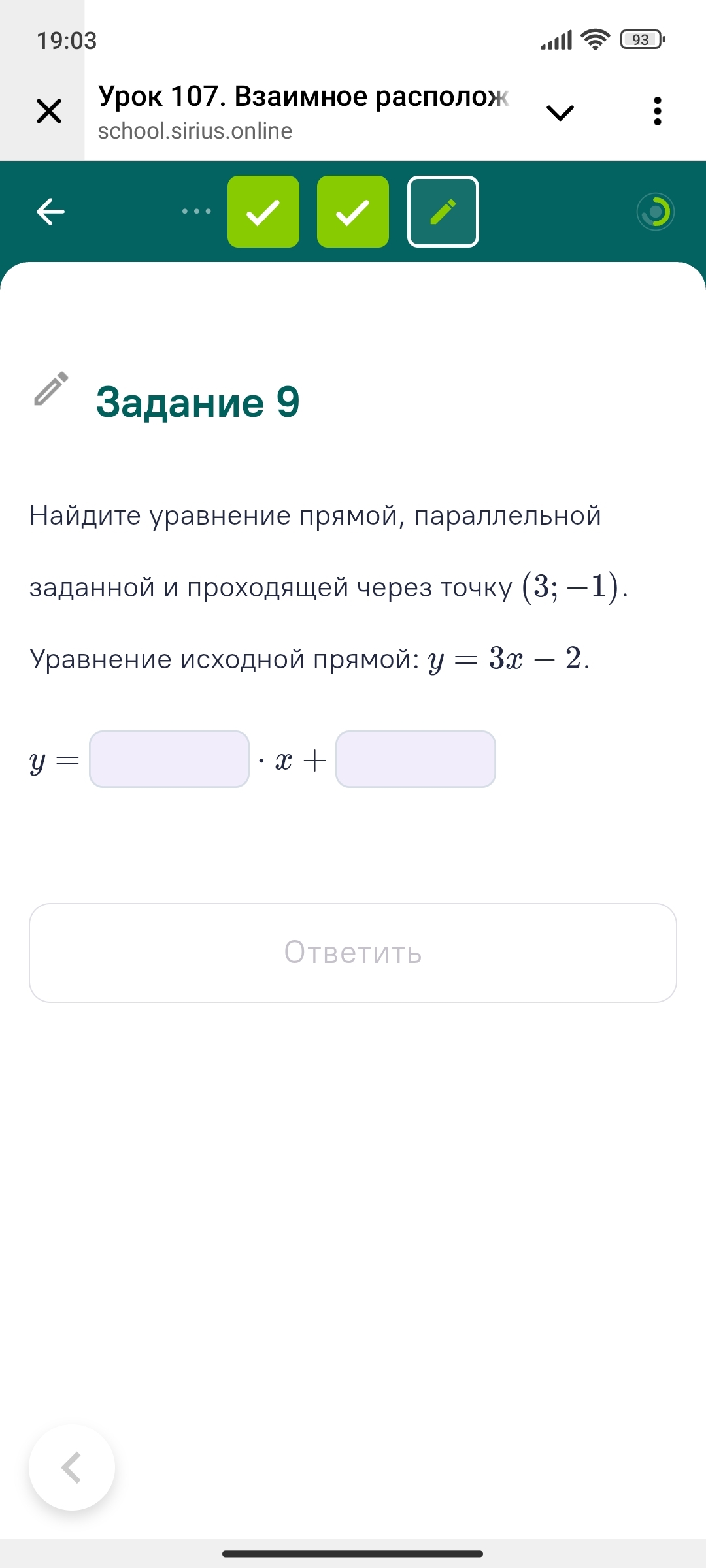
Найдите уравнение прямой, параллельной заданной и проходящей через точку (3; -1). Уравнение исходной прямой: y = 3x – 2. y = * x +

Для решения данной задачи необходимо найти уравнение прямой, параллельной заданной прямой ( y = 3x - 2 ) и проходящей через точку ( (3, -1) ). 1. Определение параллельности прямых: Параллельные прямые имеют одинаковый угловой коэффициент. В уравнении ( y = 3x - 2 ) угловой коэффициент равен 3. 2. Уравнение новой прямой: Искомая прямая будет иметь вид ( y = 3x + b ), где ( b ) - свободный член, который нужно определить. 3. Нахождение свободного члена ( b ): Прямая проходит через точку ( (3, -1) ). Подставим координаты этой точки в уравнение прямой: [ -1 = 3 cdot 3 + b ] [ -1 = 9 + b ] [ b = -1 - 9 ] [ b = -10 ] 4. Итоговое уравнение прямой: Подставим найденное значение ( b ) в уравнение прямой: [ y = 3x - 10 ] Таким образом, уравнение прямой, параллельной заданной и проходящей через точку ( (3, -1) ), имеет вид ( y = 3x - 10 ). Ответ: \(y = 3x - 10\) Ответ на пропуски: * y = 3 * x + -10 Развернутый ответ для школьника: Представь, что у тебя есть прямая линия, и тебе нужно нарисовать еще одну прямую, которая идет параллельно первой. Это значит, что они никогда не пересекутся. Если первая прямая задана уравнением ( y = 3x - 2 ), то параллельная ей прямая будет иметь вид ( y = 3x + что-то ), потому что у параллельных прямых одинаковый "наклон" (угловой коэффициент). Теперь нам нужно найти это "что-то", зная, что новая прямая проходит через точку ( (3, -1) ). Подставляем эти значения в уравнение и находим, что это "что-то" равно ( -10 ). Значит, уравнение новой прямой: ( y = 3x - 10 ).