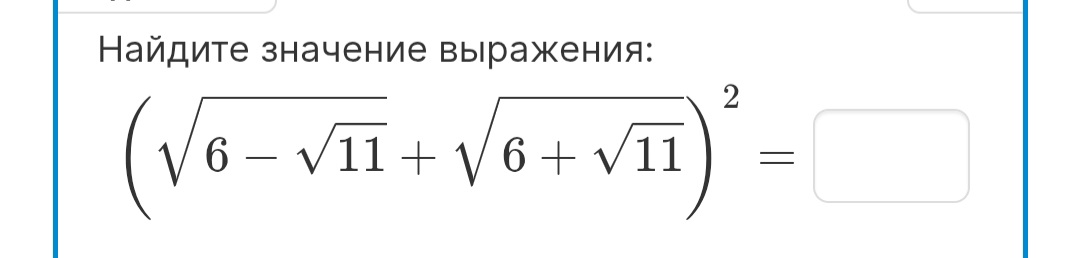
Вопрос:
Найдите значение выражения: \[(\sqrt{6 - \sqrt{11}} + \sqrt{6 + \sqrt{11}})^2 = ?\]
Ответ:
Для решения этого выражения, мы будем использовать формулу квадрата суммы: $(a + b)^2 = a^2 + 2ab + b^2$.
1. Раскроем скобки:
\[(\sqrt{6 - \sqrt{11}} + \sqrt{6 + \sqrt{11}})^2 = (\sqrt{6 - \sqrt{11}})^2 + 2(\sqrt{6 - \sqrt{11}})(\sqrt{6 + \sqrt{11}}) + (\sqrt{6 + \sqrt{11}})^2\]
2. Упростим каждый член:
* $(\sqrt{6 - \sqrt{11}})^2 = 6 - \sqrt{11}$
* $(\sqrt{6 + \sqrt{11}})^2 = 6 + \sqrt{11}$
* $2(\sqrt{6 - \sqrt{11}})(\sqrt{6 + \sqrt{11}}) = 2\sqrt{(6 - \sqrt{11})(6 + \sqrt{11})}$
3. Упростим выражение под корнем:
\[(6 - \sqrt{11})(6 + \sqrt{11}) = 6^2 - (\sqrt{11})^2 = 36 - 11 = 25\]
Тогда:
\[2\sqrt{(6 - \sqrt{11}})(6 + \sqrt{11}}) = 2\sqrt{25} = 2 \cdot 5 = 10\]
4. Подставим все упрощенные члены обратно в выражение:
\[6 - \sqrt{11} + 10 + 6 + \sqrt{11} = 6 + 10 + 6 - \sqrt{11} + \sqrt{11} = 22\]
Таким образом, значение выражения равно 22.
Ответ: 22