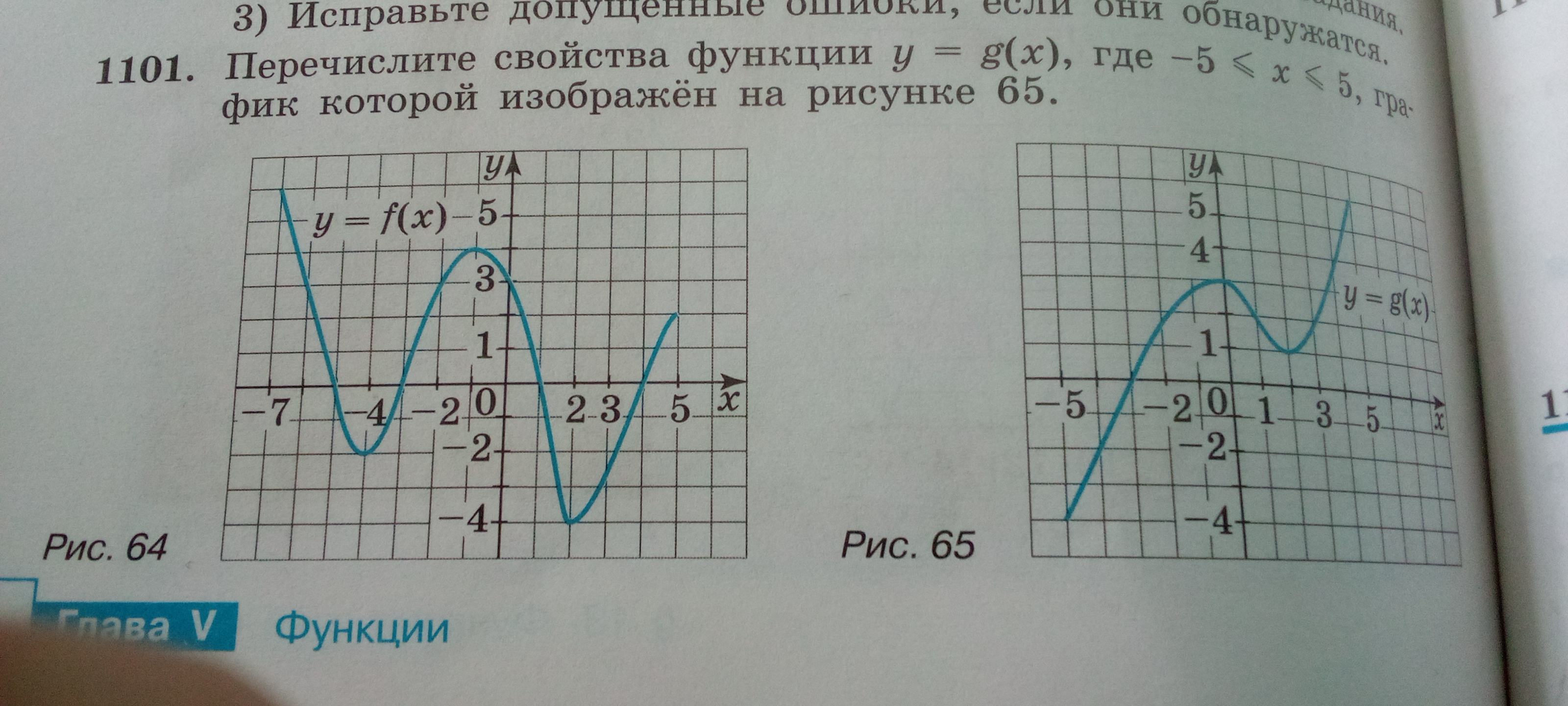
1101. Перечислите свойства функции \(y = g(x)\), где \(-5 \le x \le 5\), график которой изображён на рисунке 65.

Рассмотрим график функции \(y = g(x)\) на рисунке 65 и перечислим её свойства: 1. Область определения: Функция определена на отрезке \([-5; 5]\), то есть \(-5 \le x \le 5\). 2. Область значений: Функция принимает значения от \(-4\) до \(5\), то есть \(-4 \le y \le 5\). 3. Нули функции: График пересекает ось \(Ox\) примерно в точках \(x \approx -3\), \(x \approx 1.5\) и \(x \approx 4.5\). Значит, нули функции: \(x_1 \approx -3\), \(x_2 \approx 1.5\), \(x_3 \approx 4.5\). 4. Промежутки знакопостоянства: * \(g(x) > 0\) при \(x \in (-5; -3) \cup (1.5; 4.5)\) * \(g(x) < 0\) при \(x \in (-3; 1.5) \cup (4.5; 5)\) 5. Промежутки возрастания и убывания: * Функция убывает на промежутках \((-5; 1)\) и \((3; 5)\). * Функция возрастает на промежутке \((1; 3)\). 6. Экстремумы функции: * Точка минимума: \(x = 1\), \(y_{min} = -4\). * Точка максимума: \(x = 3\), \(y_{max} = 3\). 7. Чётность/нечётность: Функция не является ни чётной, ни нечётной, так как её график не симметричен относительно оси \(Oy\) и начала координат. Развёрнутый ответ: Для описания свойств функции \(y = g(x)\), заданной графически, мы рассмотрели следующие аспекты: область определения, область значений, нули функции, промежутки знакопостоянства, промежутки возрастания и убывания, экстремумы и чётность/нечётность. Это позволяет получить полное представление о поведении функции на заданном интервале.