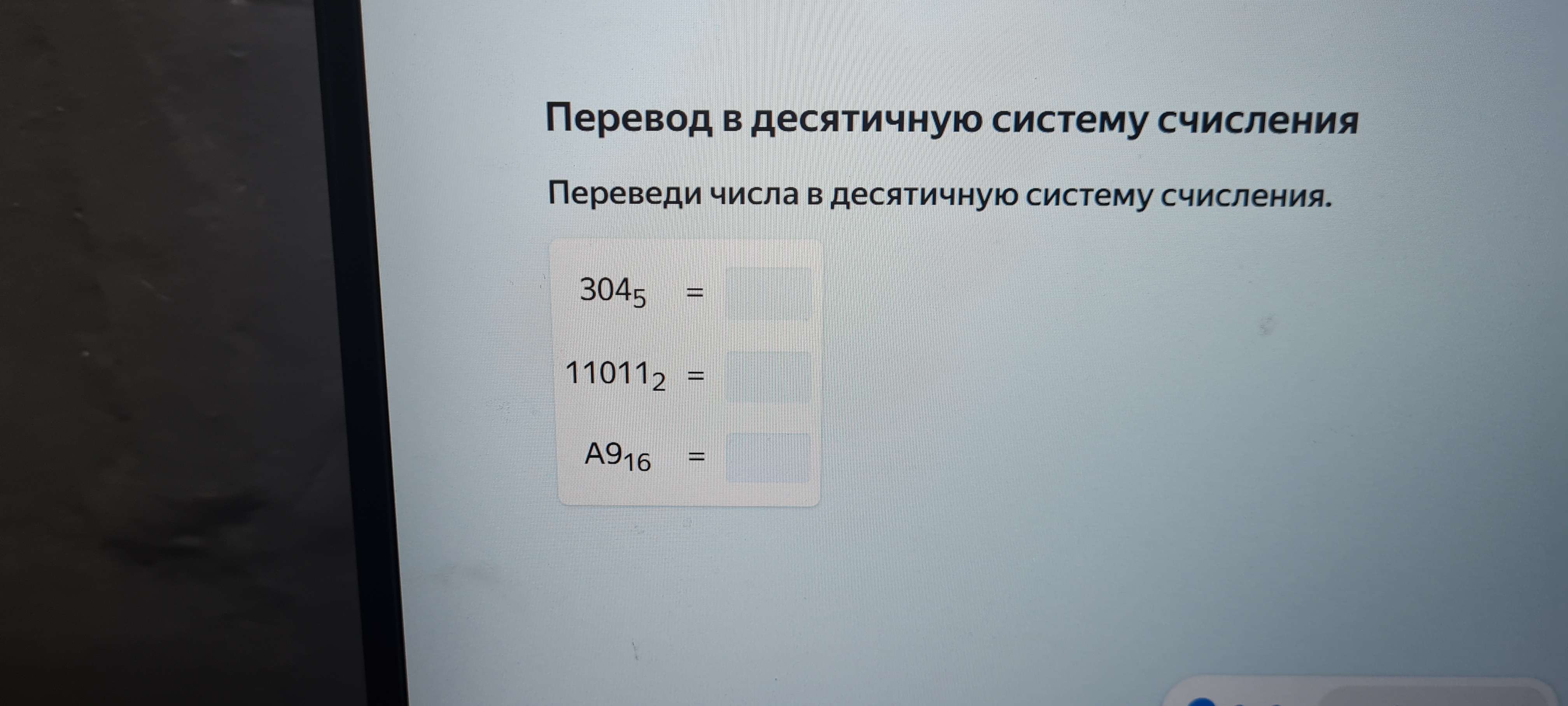
Перевод в десятичную систему счисления Переведи числа в десятичную систему счисления. 304₅ = ? 11011₂ = ? A9₁₆ = ?

Для решения этой задачи, нам нужно перевести числа из разных систем счисления в десятичную систему.

1. Перевод числа 304₅ в десятичную систему:

   Чтобы перевести число из пятеричной системы в десятичную, нужно каждый разряд умножить на соответствующую степень числа 5 и сложить результаты.

   $$304_5 = 3 \cdot 5^2 + 0 \cdot 5^1 + 4 \cdot 5^0 = 3 \cdot 25 + 0 \cdot 5 + 4 \cdot 1 = 75 + 0 + 4 = 79$$

   Ответ: 79

2. Перевод числа 11011₂ в десятичную систему:

   Чтобы перевести число из двоичной системы в десятичную, нужно каждый разряд умножить на соответствующую степень числа 2 и сложить результаты.

   $$11011_2 = 1 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 1 \cdot 16 + 1 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 1 \cdot 1 = 16 + 8 + 0 + 2 + 1 = 27$$

   Ответ: 27

3. Перевод числа A9₁₆ в десятичную систему:

   Чтобы перевести число из шестнадцатеричной системы в десятичную, нужно каждый разряд умножить на соответствующую степень числа 16 и сложить результаты. Важно помнить, что в шестнадцатеричной системе цифра 'A' соответствует числу 10.

   $$A9_{16} = 10 \cdot 16^1 + 9 \cdot 16^0 = 10 \cdot 16 + 9 \cdot 1 = 160 + 9 = 169$$

   Ответ: 169