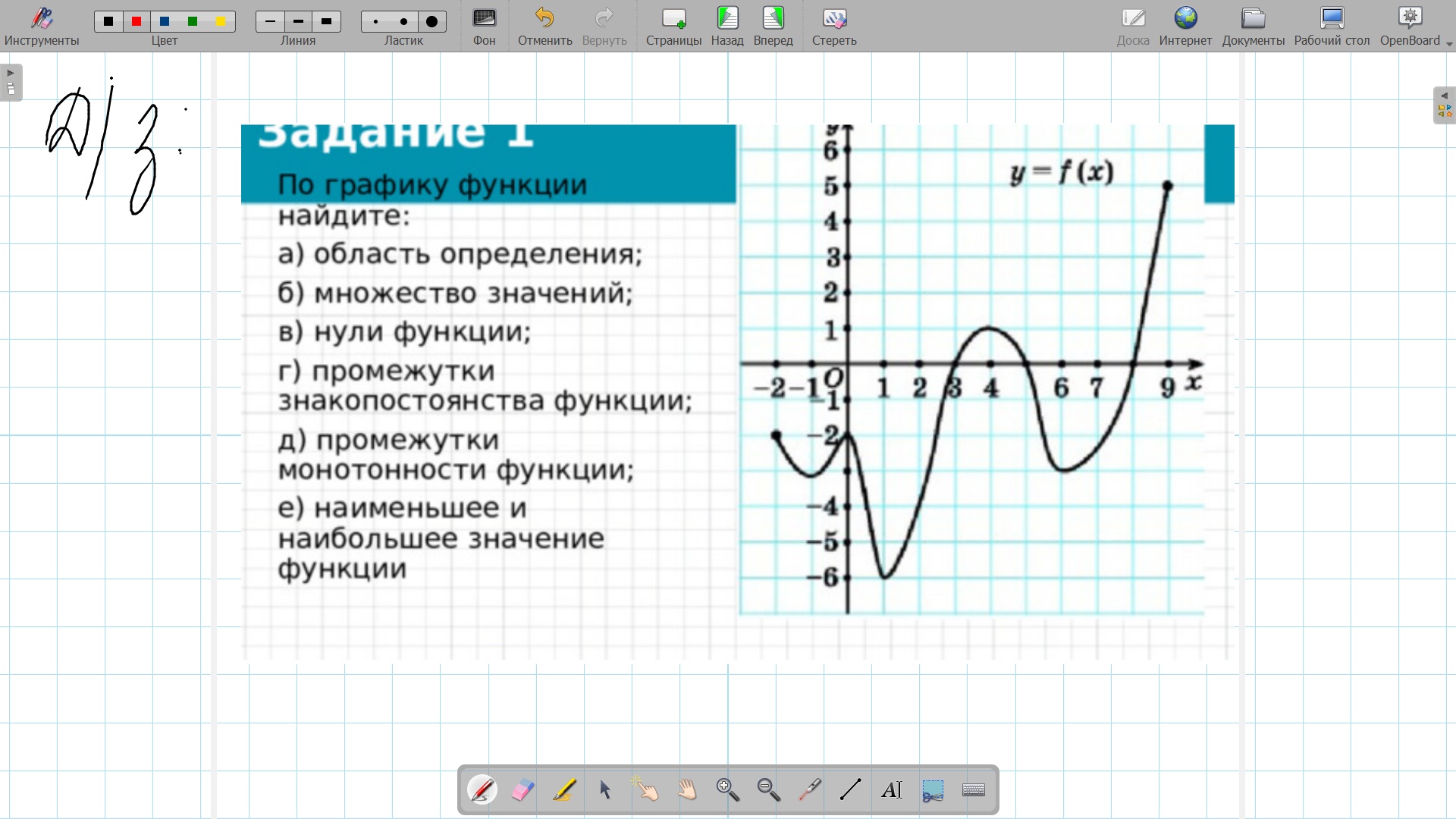
По графику функции найдите: a) область определения; б) множество значений; в) нули функции; г) промежутки знакопостоянства функции; д) промежутки монотонности функции; е) наименьшее и наибольшее значение функции

Здравствуйте, ребята! Давайте вместе решим эту задачу, используя график функции. a) Область определения функции: Область определения - это все значения x, для которых функция определена. Смотрим на график: функция определена от x = -2 до x = 9. Таким образом, область определения: \[ x \in [-2; 9] \] б) Множество значений функции: Множество значений - это все значения y, которые принимает функция. Смотрим на график: наименьшее значение y = -6, а наибольшее значение y = 6. Таким образом, множество значений: \[ y \in [-6; 6] \] в) Нули функции: Нули функции - это точки, где график пересекает ось x (то есть y = 0). На графике это точки: x = -1, x = 1.5, x = 4.5, x = 7.5 Таким образом, нули функции: \[ x = -1, 1.5, 4.5, 7.5 \] г) Промежутки знакопостоянства функции: Это интервалы, где функция больше нуля (y > 0) или меньше нуля (y < 0). * Функция положительна (y > 0): \[ x \in (-2; -1) \cup (1.5; 4.5) \cup (7.5; 9) \] * Функция отрицательна (y < 0): \[ x \in (-1; 1.5) \cup (4.5; 7.5) \] д) Промежутки монотонности функции: Это интервалы, где функция возрастает или убывает. * Функция возрастает: \[ x \in (-2; -0.2) \cup (0.5; 3) \cup (6; 9) \] * Функция убывает: \[ x \in (-0.2; 0.5) \cup (3; 6) \] е) Наименьшее и наибольшее значение функции: * Наименьшее значение функции: y = -6 (в точке x = 0.5) * Наибольшее значение функции: y = 6 (в точке x = 9) Надеюсь, теперь вам понятно, как анализировать графики функций! Если у вас возникнут вопросы, не стесняйтесь спрашивать.