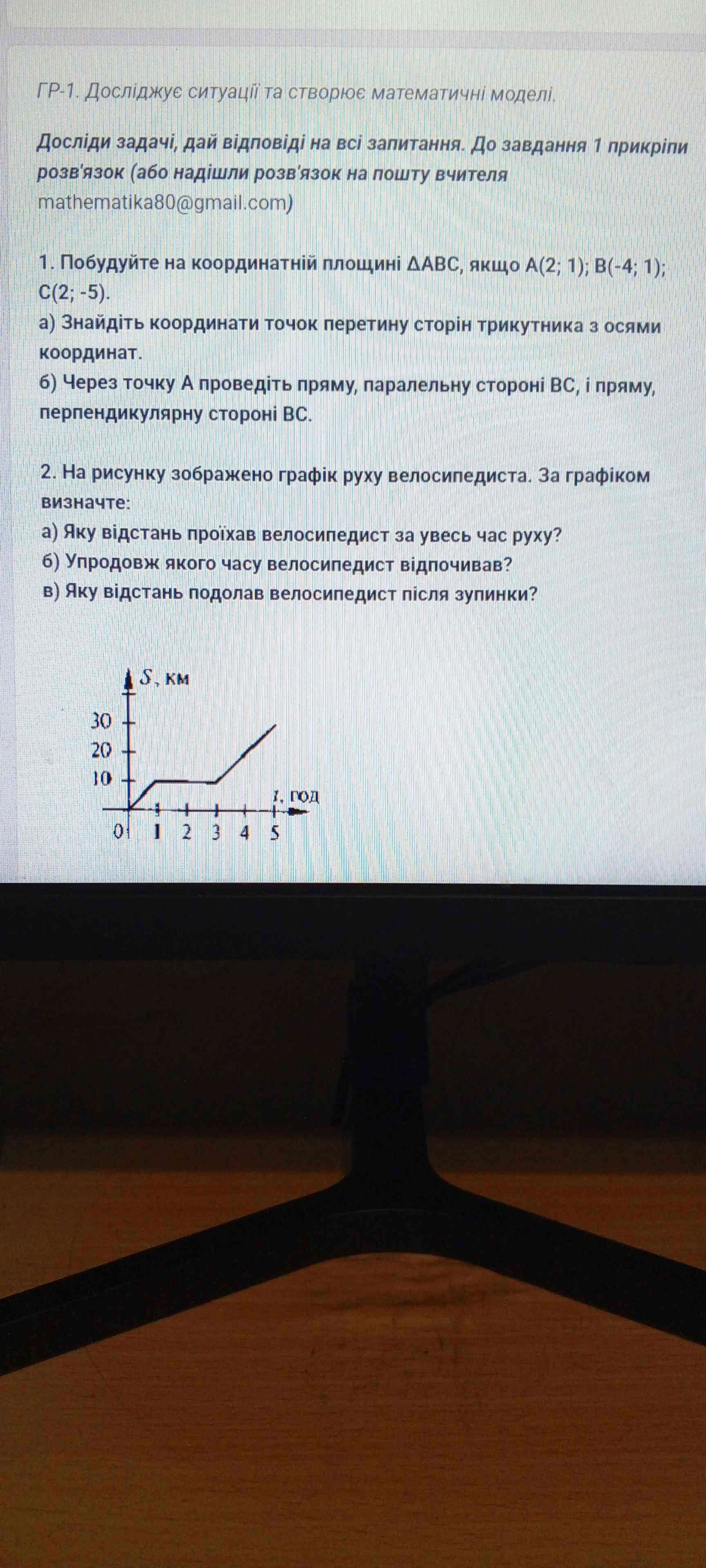
1. Побудуйте на координатній площині ΔABC, якщо A(2; 1); B(-4; 1); C(2; -5). a) Знайдіть координати точок перетину сторін трикутника з осями координат. б) Через точку A проведіть пряму, паралельну стороні BC, і пряму, перпендикулярну стороні BC. 2. На рисунку зображено графік руху велосипедиста. За графіком визначте: a) Яку відстань проїхав велосипедист за увесь час руху? б) Упродовж якого часу велосипедист відпочивав? в) Яку відстань подолав велосипедист після зупинки?

Розв'язок:

1. Побудова трикутника ΔABC на координатній площині:

Оскільки це завдання вимагає побудови, яку неможливо зобразити тут графічно, я опишу, як це зробити.

1. Намалюйте координатну площину (осі X та Y).
2. Відзначте точки A(2; 1), B(-4; 1) та C(2; -5).
3. З'єднайте ці точки, щоб утворився трикутник ΔABC.

a) Знайдіть координати точок перетину сторін трикутника з осями координат:

• Сторона AB: Оскільки y-координата точок A і B однакова (y=1), то пряма AB паралельна осі x і перетинає вісь y в точці (0;1).
• Сторона AC: Оскільки x-координата точок A і C однакова (x=2), то пряма AC паралельна осі y і перетинає вісь x в точці (2;0).
• Сторона BC: Рівняння прямої, що проходить через точки B(-4; 1) і C(2; -5), можна знайти за формулою: $$\frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}$$ $$\frac{y - 1}{-5 - 1} = \frac{x - (-4)}{2 - (-4)}$$ $$\frac{y - 1}{-6} = \frac{x + 4}{6}$$ $$y - 1 = -x - 4$$ $$y = -x - 3$$ Точка перетину з віссю x (y=0): 0 = -x - 3 => x = -3. Координати: (-3; 0). Точка перетину з віссю y (x=0): y = -0 - 3 => y = -3. Координати: (0; -3).

б) Через точку A проведіть пряму, паралельну стороні BC, і пряму, перпендикулярну стороні BC.

• Пряма, паралельна BC: Оскільки кутовий коефіцієнт прямої BC дорівнює -1, то рівняння прямої, паралельної BC і що проходить через точку A(2; 1), має вигляд: y - 1 = -1(x - 2) => y = -x + 3.
• Пряма, перпендикулярна BC: Кутовий коефіцієнт перпендикулярної прямої до BC дорівнює 1. Рівняння прямої, перпендикулярної BC і що проходить через точку A(2; 1), має вигляд: y - 1 = 1(x - 2) => y = x - 1.

2. Аналіз графіка руху велосипедиста:

a) Яку відстань проїхав велосипедист за увесь час руху?

За графіком видно, що велосипедист проїхав 30 км за весь час руху.

Відповідь: 30 км

б) Упродовж якого часу велосипедист відпочивав?

За графіком видно, що велосипедист відпочивав з 1-ї до 3-ї години. Отже, час відпочинку становить 2 години.

Відповідь: 2 години

в) Яку відстань подолав велосипедист після зупинки?

До зупинки велосипедист проїхав 10 км. Після зупинки він проїхав ще 30 - 10 = 20 км.

Відповідь: 20 км