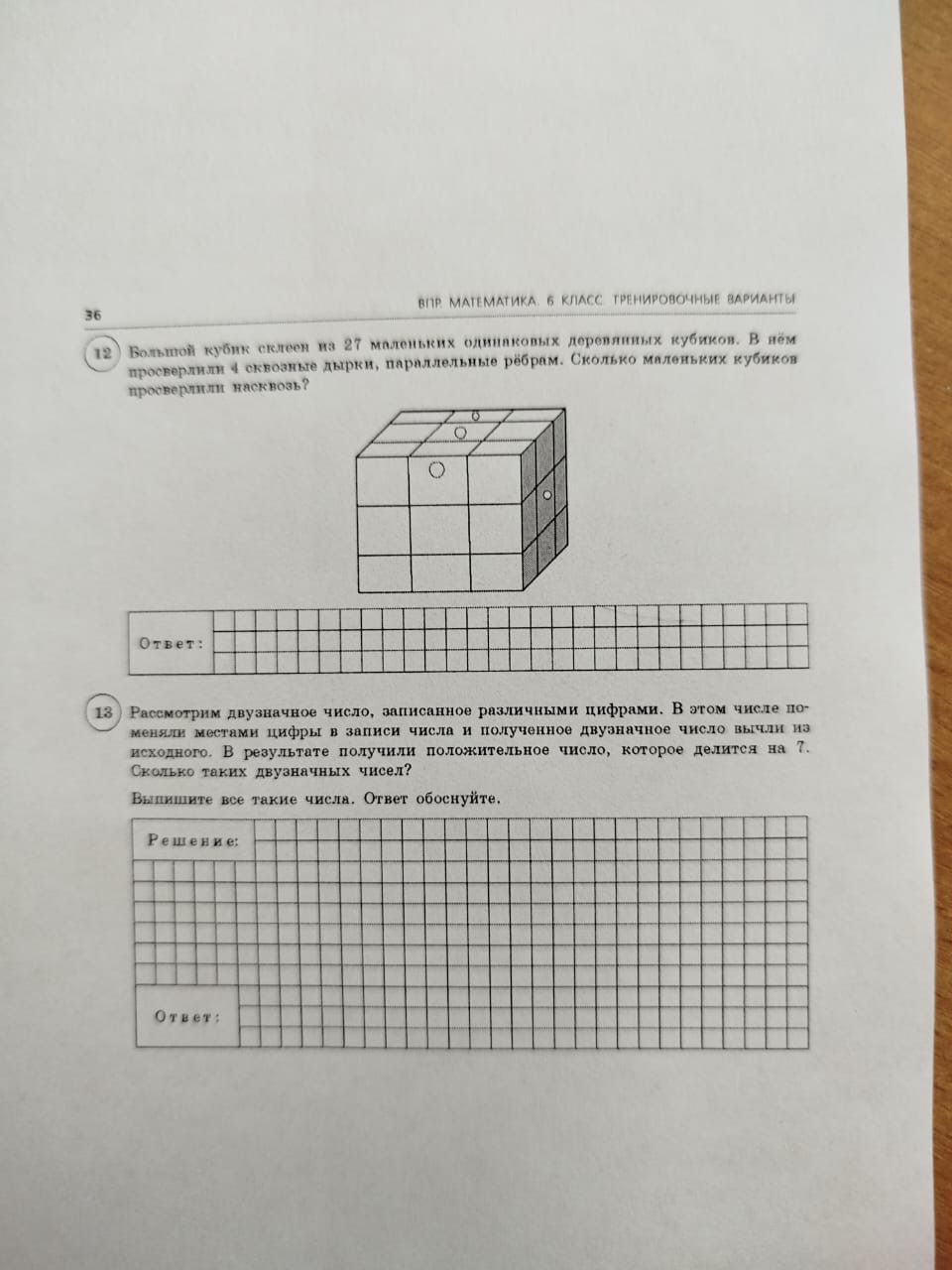
Вопрос:
Рассмотрим двузначное число, записанное различными цифрами. В этом числе поменяли местами цифры в записи числа и полученное двузначное число вычли из исходного. В результате получили положительное число, которое делится на 7. Сколько таких двузначных чисел? Выпишите все такие числа. Ответ обоснуйте.
Ответ:
Пусть двузначное число имеет вид $$\overline{ab}$$, где $$a$$ и $$b$$ - различные цифры, и $$a > b$$ (так как результат вычитания должен быть положительным).
Тогда исходное число равно $$10a + b$$, а число с переставленными цифрами равно $$10b + a$$.
Разность между исходным числом и числом с переставленными цифрами равна:
\[(10a + b) - (10b + a) = 10a + b - 10b - a = 9a - 9b = 9(a - b).\]
По условию, эта разность делится на 7, то есть $$9(a - b)$$ делится на 7. Поскольку 9 и 7 - взаимно простые числа, то $$(a - b)$$ должно делиться на 7. Так как $$a$$ и $$b$$ - цифры, то $$a - b$$ может быть равно 7. (так как разность не может быть 0, потому что цифры различные)
Найдем все пары цифр $$a$$ и $$b$$ такие, что $$a - b = 7$$:
* Если $$b = 0$$, то $$a = 7$$. Число 70.
* Если $$b = 1$$, то $$a = 8$$. Число 81.
* Если $$b = 2$$, то $$a = 9$$. Число 92.
Проверим:
* $$70 - 07 = 63 = 7 * 9$$
* $$81 - 18 = 63 = 7 * 9$$
* $$92 - 29 = 63 = 7 * 9$$
Таким образом, существует 3 таких двузначных числа: 70, 81 и 92.
Ответ: 3 числа (70, 81, 92)