Вопрос:
8. Реши задачу. Радиоактивный изотоп кобальт-60 (\(^{60}_{27}Co\)) используется в медицинских приборах ядерной энергетики. Его период полураспада составляет 5,27 лет. Начальная масса образца 32 г. Сколько вещества останется через 15,81 года? Как это связано с безопасностью для живых организмов?
Ответ:
Решение:
Период полураспада \(T_{1/2} = 5.27\) лет.
Время \(t = 15.81\) лет.
Начальная масса \(m_0 = 32\) г.
Количество периодов полураспада:
\[n = \frac{t}{T_{1/2}} = \frac{15.81}{5.27} = 3\]
Масса вещества после 3 периодов полураспада:
\[m = m_0 \cdot \left(\frac{1}{2}\right)^n = 32 \cdot \left(\frac{1}{2}\right)^3 = 32 \cdot \frac{1}{8} = 4\ \text{г}\]
Ответ: Через 15,81 года останется 4 г кобальта-60.
Связь с безопасностью:
Уменьшение массы радиоактивного изотопа со временем делает его менее опасным, так как снижается интенсивность излучения. Однако, даже небольшое количество радиоактивного вещества может представлять опасность при неправильном обращении.
Похожие
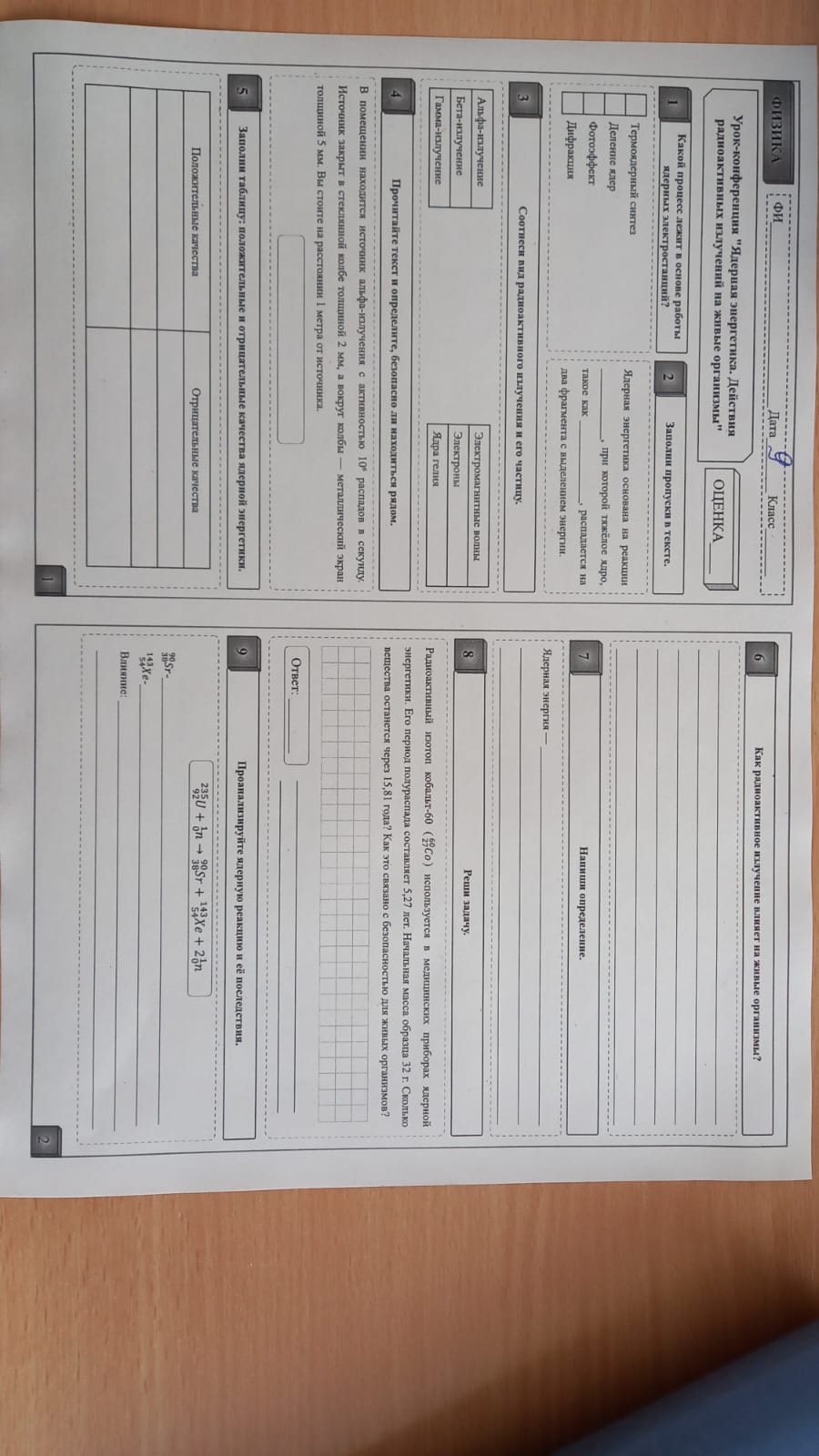
- 1. Какой процесс лежит в основе работы ядерных электростанций?
- 2. Заполни пропуски в тексте.
- 3. Соотнеси вид радиоактивного излучения и его частицу.
- 4. Прочитайте текст и определите, безопасно ли находиться рядом.
- 5. Заполни таблицу: положительные и отрицательные качества ядерной энергетики.
- 6. Как радиоактивное излучение влияет на живые организмы?
- 7. Напиши определение. Ядерная энергия -
- 8. Реши задачу. Радиоактивный изотоп кобальт-60 (\(^{60}_{27}Co\)) используется в медицинских приборах ядерной энергетики. Его период полураспада составляет 5,27 лет. Начальная масса образца 32 г. Сколько вещества останется через 15,81 года? Как это связано с безопасностью для живых организмов?
- 9. Проанализируйте ядерную реакцию и её последствия. \(^{235}_{92}U + ^1_0n \rightarrow ^{90}_{38}Sr + ^{143}_{54}Xe + 2 ^1_0n\) \(^{90}_{38}Sr\)- \(^{143}_{54}Xe\)- Влияние: