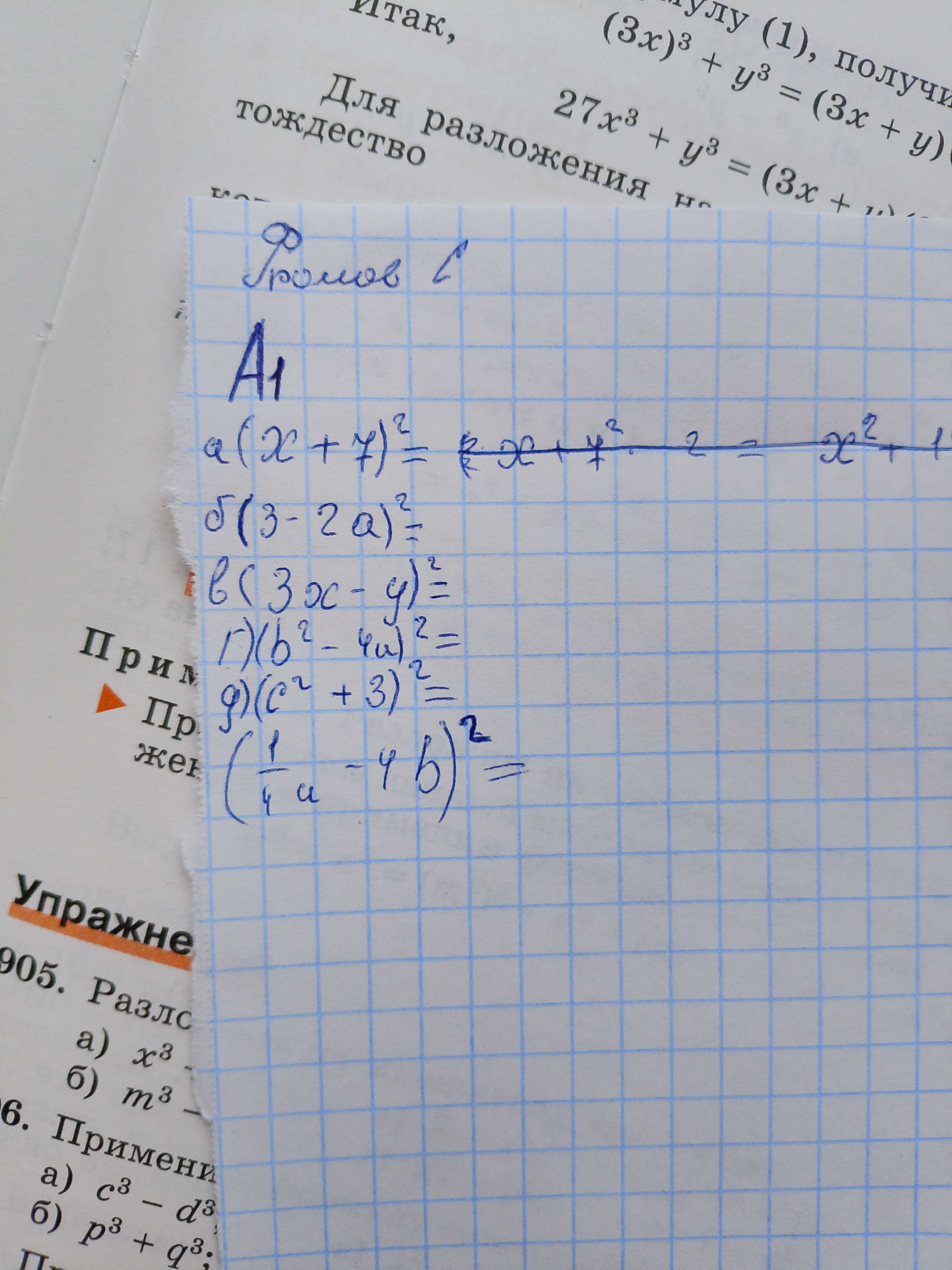
Решите примеры, используя формулу сокращенного умножения: квадрат суммы/разности. a) $$(x+y)^2$$ б) $$(3-2a)^2$$ в) $$(3x-y)^2$$ г) $$(b^2-4a)^2$$ д) $$(c^2+3)^2$$ e) $$(\frac{1}{4}u - 4b)^2$$

Привет! Сейчас мы решим эти примеры, применяя формулы сокращенного умножения. Вспомним основные формулы квадрата суммы и квадрата разности:

Квадрат суммы: $$(a + b)^2 = a^2 + 2ab + b^2$$

Квадрат разности: $$(a - b)^2 = a^2 - 2ab + b^2$$

Теперь решим каждый пример по порядку:

1. a) $$(x+y)^2$$

   Используем формулу квадрата суммы: $$(a + b)^2 = a^2 + 2ab + b^2$$

   Подставляем x и y вместо a и b: $$(x + y)^2 = x^2 + 2xy + y^2$$

   Ответ: $$x^2 + 2xy + y^2$$

2. б) $$(3-2a)^2$$

   Используем формулу квадрата разности: $$(a - b)^2 = a^2 - 2ab + b^2$$

   Подставляем 3 и 2a вместо a и b: $$(3 - 2a)^2 = 3^2 - 2 cdot 3 cdot 2a + (2a)^2$$

   Упрощаем: $$9 - 12a + 4a^2$$

   Ответ: $$9 - 12a + 4a^2$$

3. в) $$(3x-y)^2$$

   Используем формулу квадрата разности: $$(a - b)^2 = a^2 - 2ab + b^2$$

   Подставляем 3x и y вместо a и b: $$(3x - y)^2 = (3x)^2 - 2 cdot 3x cdot y + y^2$$

   Упрощаем: $$9x^2 - 6xy + y^2$$

   Ответ: $$9x^2 - 6xy + y^2$$

4. г) $$(b^2-4a)^2$$

   Используем формулу квадрата разности: $$(a - b)^2 = a^2 - 2ab + b^2$$

   Подставляем $$b^2$$ и 4a вместо a и b: $$(b^2 - 4a)^2 = (b^2)^2 - 2 cdot b^2 cdot 4a + (4a)^2$$

   Упрощаем: $$b^4 - 8ab^2 + 16a^2$$

   Ответ: $$b^4 - 8ab^2 + 16a^2$$

5. д) $$(c^2+3)^2$$

   Используем формулу квадрата суммы: $$(a + b)^2 = a^2 + 2ab + b^2$$

   Подставляем $$c^2$$ и 3 вместо a и b: $$(c^2 + 3)^2 = (c^2)^2 + 2 cdot c^2 cdot 3 + 3^2$$

   Упрощаем: $$c^4 + 6c^2 + 9$$

   Ответ: $$c^4 + 6c^2 + 9$$

6. е) $$(\frac{1}{4}u - 4b)^2$$

   Используем формулу квадрата разности: $$(a - b)^2 = a^2 - 2ab + b^2$$

   Подставляем $$(\frac{1}{4}u)$$ и 4b вместо a и b: $$((\frac{1}{4}u) - 4b)^2 = (\frac{1}{4}u)^2 - 2 cdot (\frac{1}{4}u) cdot 4b + (4b)^2$$

   Упрощаем: $$\frac{1}{16}u^2 - 2ub + 16b^2$$

   Ответ: $$\frac{1}{16}u^2 - 2ub + 16b^2$$