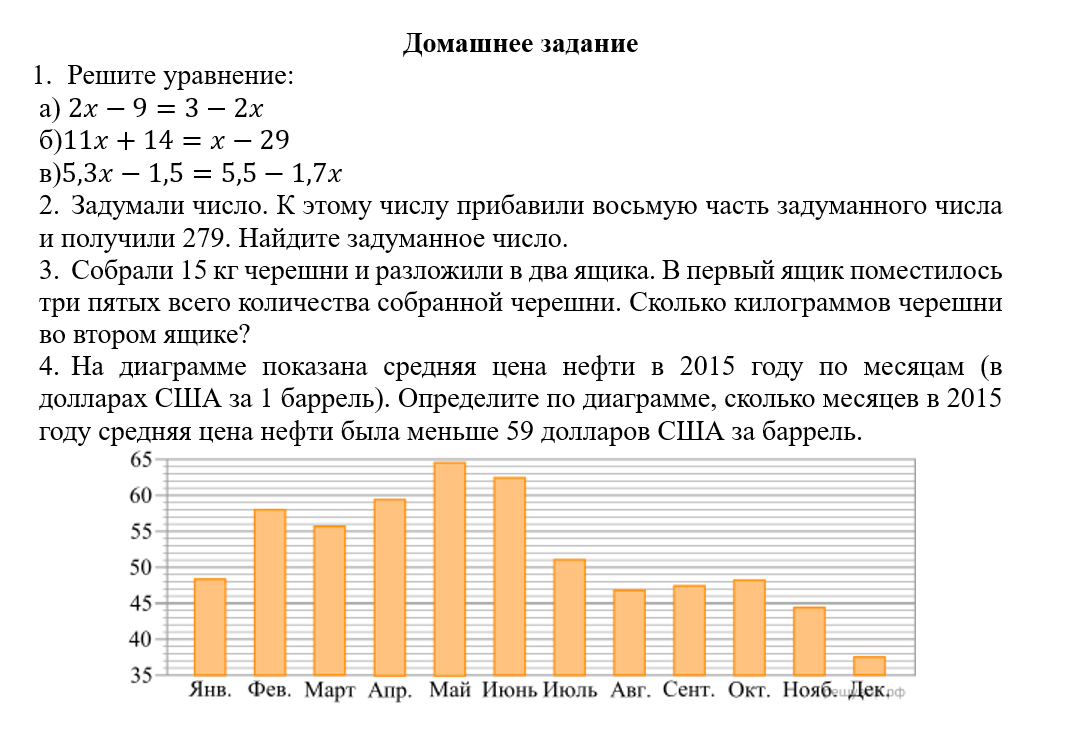
1. Решите уравнение: a) $$2x - 9 = 3 - 2x$$ б) $$11x + 14 = x - 29$$ в) $$5,3x - 1,5 = 5,5 - 1,7x$$ 2. Задумали число. К этому числу прибавили восьмую часть задуманного числа и получили 279. Найдите задуманное число. 3. Собрали 15 кг черешни и разложили в два ящика. В первый ящик поместилось три пятых всего количества собранной черешни. Сколько килограммов черешни во втором ящике? 4. На диаграмме показана средняя цена нефти в 2015 году по месяцам (в долларах США за 1 баррель). Определите по диаграмме, сколько месяцев в 2015 году средняя цена нефти была меньше 59 долларов США за баррель.

Решение: 1. Решим уравнения: a) $$2x - 9 = 3 - 2x$$ Перенесем все члены с $$x$$ в левую часть, а числа в правую часть: $$2x + 2x = 3 + 9$$ $$4x = 12$$ $$x = \frac{12}{4}$$ $$x = 3$$ Ответ: $$x = 3$$ б) $$11x + 14 = x - 29$$ Перенесем все члены с $$x$$ в левую часть, а числа в правую часть: $$11x - x = -29 - 14$$ $$10x = -43$$ $$x = \frac{-43}{10}$$ $$x = -4,3$$ Ответ: $$x = -4,3$$ в) $$5,3x - 1,5 = 5,5 - 1,7x$$ Перенесем все члены с $$x$$ в левую часть, а числа в правую часть: $$5,3x + 1,7x = 5,5 + 1,5$$ $$7x = 7$$ $$x = \frac{7}{7}$$ $$x = 1$$ Ответ: $$x = 1$$ 2. Решим задачу: Пусть задуманное число равно $$x$$. Тогда, согласно условию, имеем уравнение: $$x + \frac{1}{8}x = 279$$ Умножим обе части уравнения на 8: $$8x + x = 279 \cdot 8$$ $$9x = 2232$$ $$x = \frac{2232}{9}$$ $$x = 248$$ Ответ: Задуманное число равно 248. 3. Решим задачу: Общее количество черешни: 15 кг. В первом ящике: $$\frac{3}{5}$$ от 15 кг. Найдем, сколько кг черешни в первом ящике: $$\frac{3}{5} \cdot 15 = \frac{3 \cdot 15}{5} = 3 \cdot 3 = 9$$ кг. Во втором ящике: общее количество минус количество в первом ящике: $$15 - 9 = 6$$ кг. Ответ: Во втором ящике 6 кг черешни. 4. Решим задачу: По диаграмме нужно определить, сколько месяцев в 2015 году средняя цена нефти была меньше 59 долларов США за баррель. Визуально оценим столбцы диаграммы: Январь: около 49 долларов. Февраль: около 58 долларов. Март: около 56 долларов. Апрель: около 59 долларов. Май: около 64 долларов. Июнь: около 63 долларов. Июль: около 51 долларов. Август: около 47 долларов. Сентябрь: около 48 долларов. Октябрь: около 49 долларов. Ноябрь: около 37 долларов. Декабрь: около 36 долларов. Месяцы, когда цена была меньше 59 долларов: Январь, Февраль, Март, Июль, Август, Сентябрь, Октябрь, Ноябрь, Декабрь. Всего таких месяцев 9. Ответ: 9 месяцев.