Вопрос:
9. Тип 8 № 1822 Из маленьких кубиков собрали параллелепипед (см. рис.). Его покрасили снаружи со всех сторон. Когда краска высохла, параллелепипед разобрали на кубики. Сколько получилось кубиков, у которых окрашены ровно две грани?
Ответ:
Считаем, что параллелепипед имеет размеры 3х4х5 кубиков. Кубики, у которых окрашены ровно две грани, находятся на ребрах параллелепипеда, но не в углах.
У параллелепипеда есть 4 ребра длиной 3 кубика, 4 ребра длиной 4 кубика, и 4 ребра длиной 5 кубиков.
На каждом ребре длиной 3 кубика есть 1 кубик с двумя окрашенными гранями (3-2=1).
На каждом ребре длиной 4 кубика есть 2 кубика с двумя окрашенными гранями (4-2=2).
На каждом ребре длиной 5 кубиков есть 3 кубика с двумя окрашенными гранями (5-2=3).
Всего кубиков с двумя окрашенными гранями: $$4 \cdot 1 + 4 \cdot 2 + 4 \cdot 3 = 4 + 8 + 12 = 24$$.
Ответ: 24 кубика
Похожие
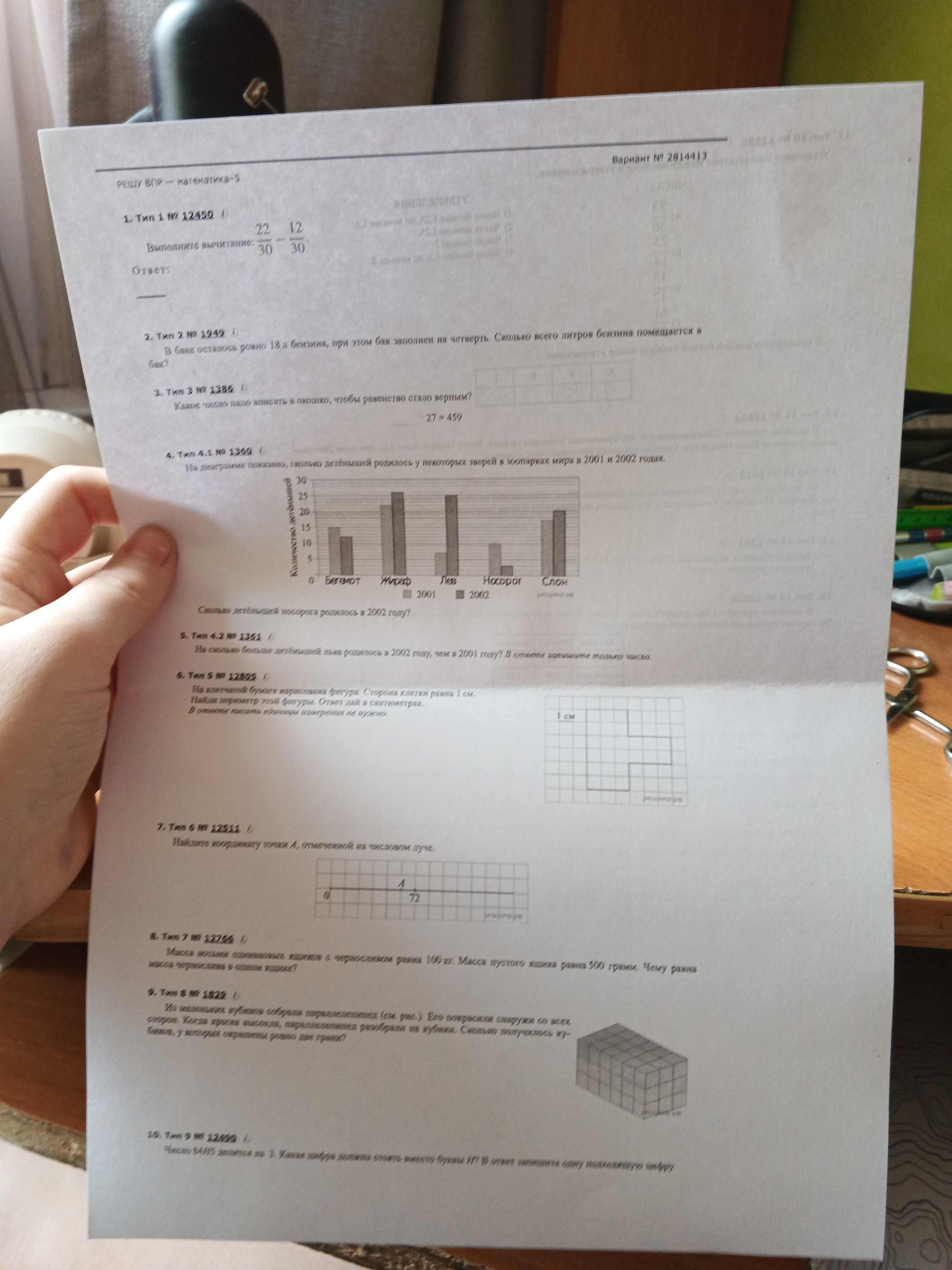
- 1. Тип 1 № 12450 Выполните вычитание: $\frac{22}{30} - \frac{12}{30}$
- 2. Тип 2 № 1949 В баке осталось ровно 18 л бензина, при этом бак заполнен на четверть. Сколько всего литров бензина помещается в бак?
- 3. Тип 3 № 1386 Какое число надо вписать в окошко, чтобы равенство стало верным? $\boxed{?} \cdot 27 = 459$
- 4. Тип 4.1 № 1360 На диаграмме показано, сколько детёнышей родилось у некоторых зверей в зоопарках мира в 2001 и 2002 годах. Сколько детёнышей носорога родилось в 2002 году?
- 5. Тип 4.2 № 1361 На сколько больше детёнышей льва родилось в 2002 году, чем в 2001 году? В ответе запишите только число.
- 6. Тип 5 № 12805 На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см. Найди периметр этой фигуры. Ответ дай в сантиметрах. В ответе писать единицы измерения не нужно.
- 7. Тип 6 № 12511 Найдите координату точки А, отмеченной на числовом луче.
- 8. Тип 7 № 12756 Масса восьми одинаковых ящиков с черносливом равна 100 кг. Масса пустого ящика равна 500 грамм. Чему равна масса чернослива в одном ящике?
- 9. Тип 8 № 1822 Из маленьких кубиков собрали параллелепипед (см. рис.). Его покрасили снаружи со всех сторон. Когда краска высохла, параллелепипед разобрали на кубики. Сколько получилось кубиков, у которых окрашены ровно две грани?
- 10. Тип 9 № 12499 Число 84\_5 делится на 3. Какая цифра должна стоять вместо буквы П? В ответ запишите одну подходящую цифру.