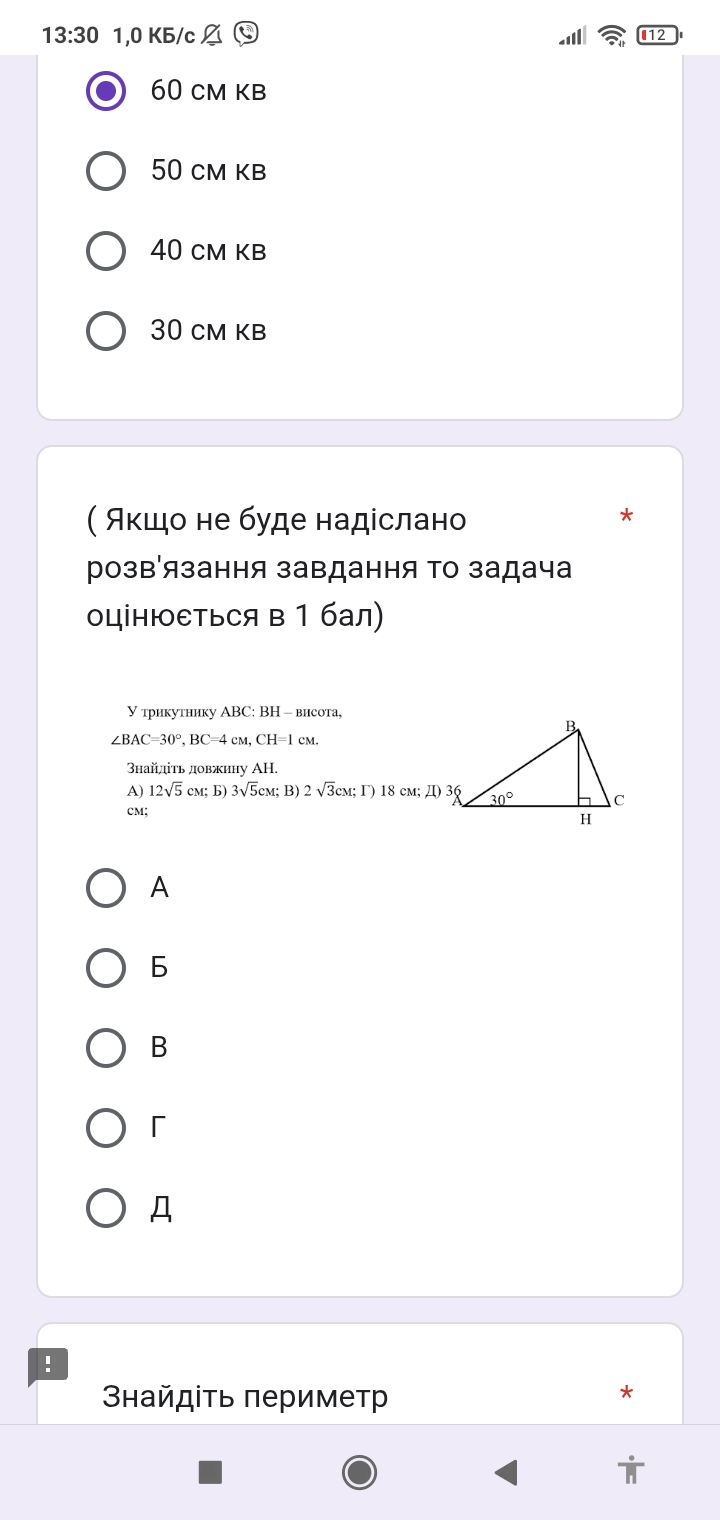
У трикутнику АВС: ВН - висота, ∠BAC=30°, ВС=4 см, СН=1 см. Знайдіть довжину АН. А) 12√5 см; Б) 3√5см; В) 2 √3см; Г) 18 см; Д) 36 см;

Розглянемо трикутник BHC. Він прямокутний, оскільки BH - висота. Ми знаємо, що BC = 4 см і CH = 1 см. Тоді, за теоремою Піфагора, ми можемо знайти BH:

$$BH^2 + CH^2 = BC^2$$

$$BH^2 + 1^2 = 4^2$$

$$BH^2 + 1 = 16$$

$$BH^2 = 15$$

$$BH = \sqrt{15}$$

Тепер розглянемо трикутник ABH. Він також прямокутний, оскільки BH - висота. Ми знаємо, що ∠BAH = 30° і BH = √15. Ми можемо використовувати тангенс кута BAH, щоб знайти AH:

$$tg(∠BAH) = \frac{BH}{AH}$$

$$tg(30°) = \frac{\sqrt{15}}{AH}$$

Ми знаємо, що $$tg(30°) = \frac{1}{\sqrt{3}}$$. Тоді:

$$\frac{1}{\sqrt{3}} = \frac{\sqrt{15}}{AH}$$

$$AH = \sqrt{15} * \sqrt{3}$$

$$AH = \sqrt{45}$$

$$AH = \sqrt{9 * 5}$$

$$AH = 3\sqrt{5}$$

Отже, довжина AH = 3√5 см.

Відповідь: Б) 3√5 см