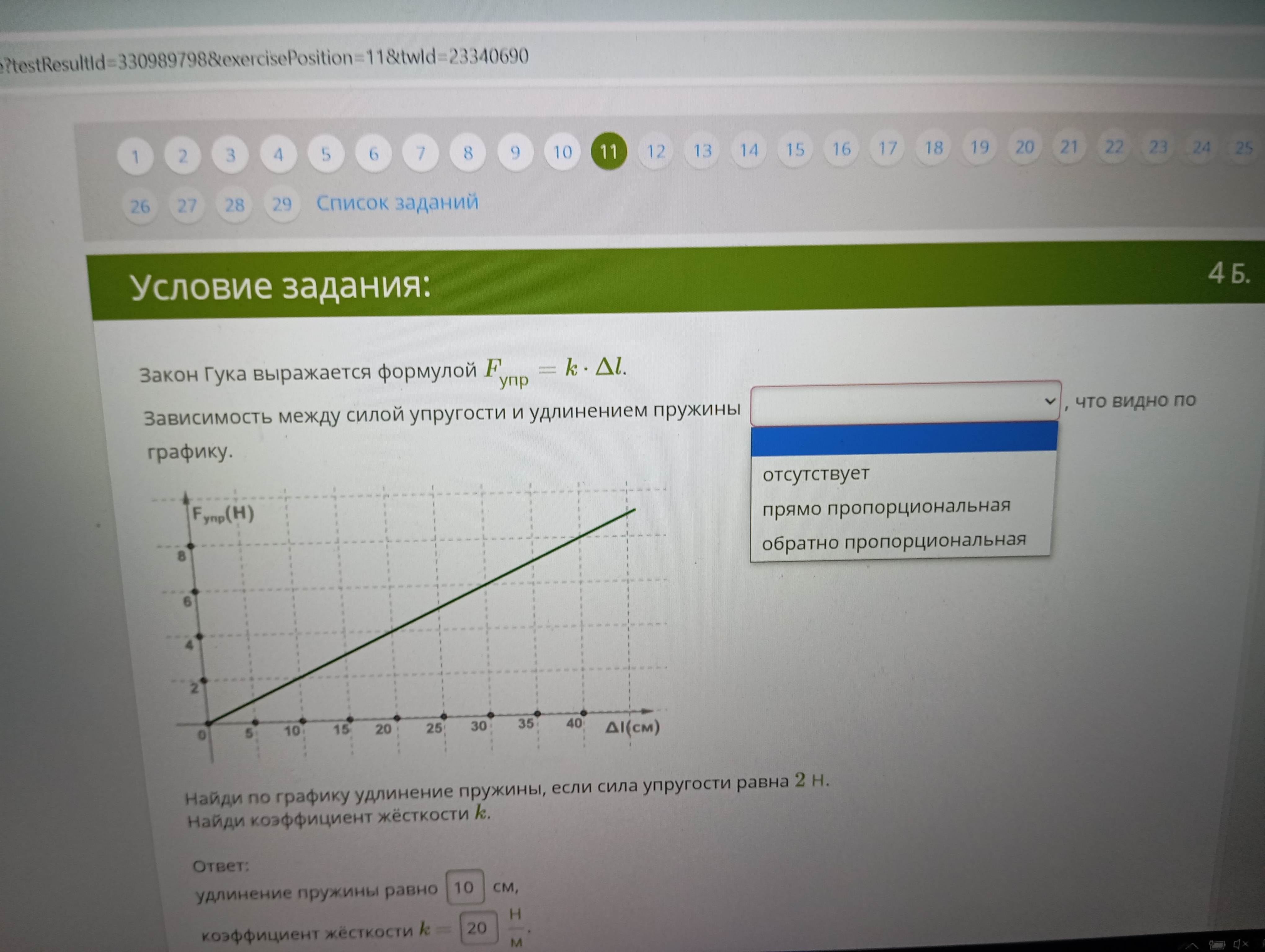
Условие задания: Закон Гука выражается формулой $$F_{упр} = k \cdot \Delta l$$. Зависимость между силой упругости и удлинением пружины ..., что видно по графику. Найди по графику удлинение пружины, если сила упругости равна 2 Н. Найди коэффициент жёсткости k. Ответ: удлинение пружины равно ... см, коэффициент жёсткости k = ... H/M

Закон Гука утверждает, что сила упругости, возникающая в деформированном теле, прямо пропорциональна величине деформации. Это означает, что чем больше мы растягиваем или сжимаем пружину, тем больше сила, которая стремится вернуть её в исходное состояние. Из графика видно, что зависимость между силой упругости и удлинением пружины прямо пропорциональная.

Теперь решим задачу, используя график и формулу закона Гука.

1. Находим удлинение пружины при силе упругости 2 Н.

По графику видно, что силе упругости в 2 Н соответствует удлинение пружины в 10 см.

2. Вычисляем коэффициент жёсткости пружины.

Из закона Гука $$F_{упр} = k \cdot \Delta l$$ выразим коэффициент жёсткости:

$$k = \frac{F_{упр}}{\Delta l}$$

Подставим известные значения силы упругости (2 Н) и удлинения (10 см = 0,1 м):

$$k = \frac{2 \text{ Н}}{0.1 \text{ м}} = 20 \text{ Н/м}$$

Ответ:

Удлинение пружины равно 10 см.

Коэффициент жёсткости пружины равен 20 Н/м.