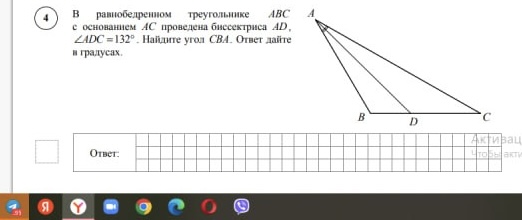
В равнобедренном треугольнике ABC с основанием AC проведена биссектриса AD, \(\angle ADC = 132^\circ\). Найдите угол CBA. Ответ дайте в градусах.

Давайте решим эту задачу по шагам. 1. Анализ условия: * Треугольник \(ABC\) равнобедренный, значит, \(AB = BC\). Следовательно, углы при основании \(\angle BAC = \angle BCA\). * \(AD\) - биссектриса угла \(\angle BAC\), значит, \(\angle BAD = \angle CAD\). * Известно, что \(\angle ADC = 132^\circ\). 2. Найдем угол \(\angle CAD\): * Угол \(\angle ADC\) и угол \(\angle ADB\) - смежные, значит их сумма равна \(180^\circ\). \[\angle ADB = 180^\circ - \angle ADC = 180^\circ - 132^\circ = 48^\circ\] 3. Рассмотрим треугольник \(ABD\): * Сумма углов в треугольнике равна \(180^\circ\). \[\angle BAD + \angle ABD + \angle ADB = 180^\circ\] * Выразим \(\angle BAD\): \[\angle BAD = 180^\circ - \angle ABD - \angle ADB\] 4. Обозначим углы: * Пусть \(\angle BAC = x\). Так как \(AD\) - биссектриса, то \(\angle BAD = \frac{x}{2}\). * \(\angle CBA = \angle ABD\) (угол \(\angle CBA\) и угол \(\angle ABD\) это один и тот же угол). 5. Выразим \(\angle BAC\): * Так как \(\angle BAD = 180^\circ - \angle ABD - \angle ADB\), то \[\frac{x}{2} = 180^\circ - \angle ABD - 48^\circ\] \[\frac{x}{2} = 132^\circ - \angle ABD\] \[x = 264^\circ - 2 \cdot \angle ABD\] 6. Рассмотрим треугольник \(ABC\): * Сумма углов в треугольнике равна \(180^\circ\). \[\angle BAC + \angle BCA + \angle CBA = 180^\circ\] * Так как треугольник равнобедренный, \(\angle BAC = \angle BCA = x\). \[x + x + \angle CBA = 180^\circ\] \[2x + \angle CBA = 180^\circ\] 7. Подставим значение \(x\): \[2(264^\circ - 2 \cdot \angle CBA) + \angle CBA = 180^\circ\] \[528^\circ - 4 \cdot \angle CBA + \angle CBA = 180^\circ\] \[528^\circ - 3 \cdot \angle CBA = 180^\circ\] \[3 \cdot \angle CBA = 528^\circ - 180^\circ\] \[3 \cdot \angle CBA = 348^\circ\] \[\angle CBA = \frac{348^\circ}{3}\] \[\angle CBA = 116^\circ\] Ответ: \(116^\circ\).