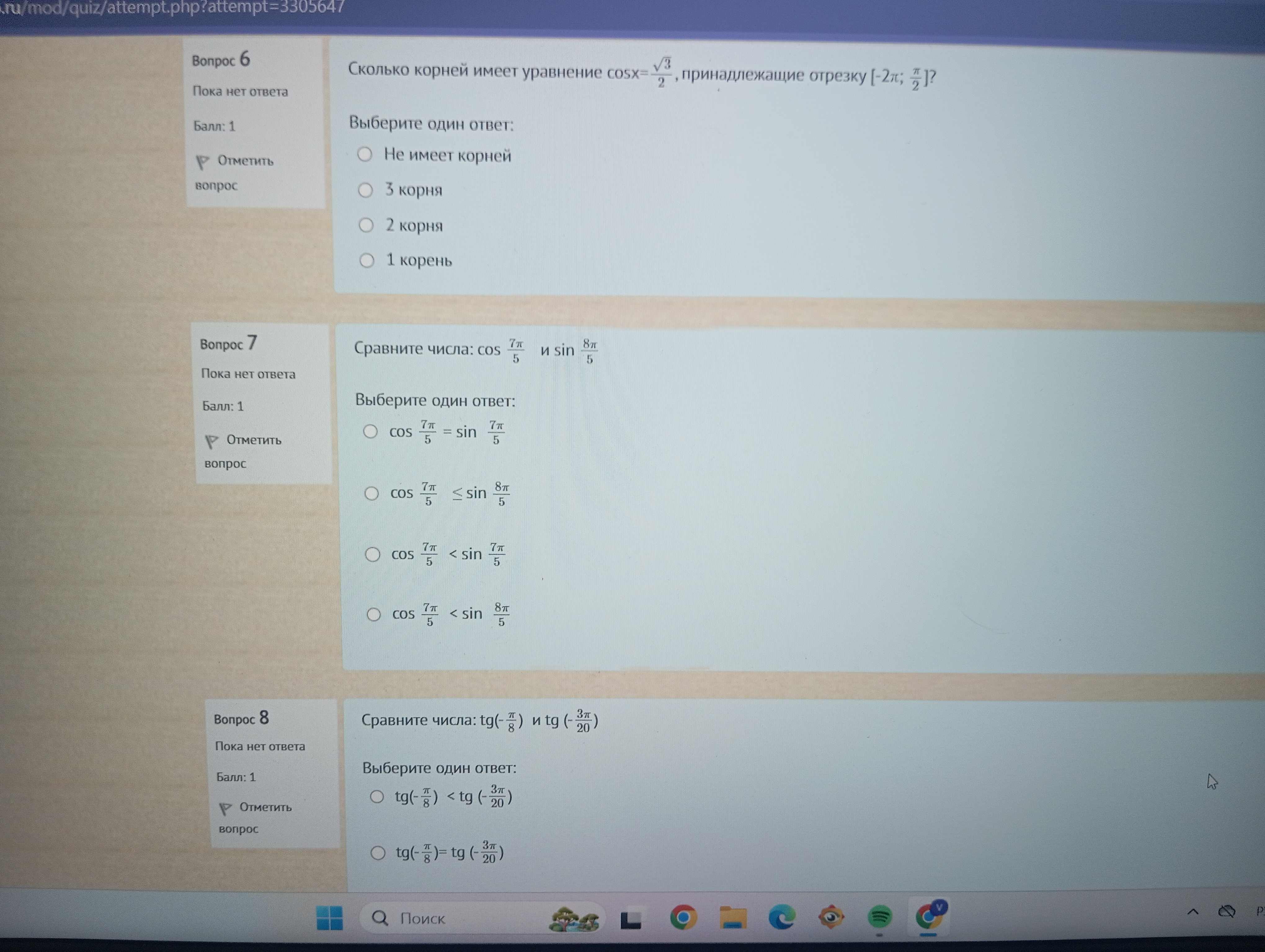
Вопрос 8: Сравните числа: $$tg(-\frac{\pi}{8})$$ и $$tg(-\frac{3\pi}{20})$$

Для решения задачи нужно сравнить значения $$tg(-\frac{\pi}{8})$$ и $$tg(-\frac{3\pi}{20})$$. 1. Учитывая, что тангенс - нечетная функция, $$tg(-x) = -tg(x)$$, можем переписать выражение как $$-tg(\frac{\pi}{8})$$ и $$-tg(\frac{3\pi}{20})$$. 2. Теперь сравним $$tg(\frac{\pi}{8})$$ и $$tg(\frac{3\pi}{20})$$. Так как тангенс возрастает в первой четверти, нужно сравнить углы $$\frac{\pi}{8}$$ и $$\frac{3\pi}{20}$$. 3. Приведем дроби к общему знаменателю: $$\frac{\pi}{8} = \frac{5\pi}{40}$$ и $$\frac{3\pi}{20} = \frac{6\pi}{40}$$. 4. Сравним $$\frac{5\pi}{40}$$ и $$\frac{6\pi}{40}$$. Очевидно, что $$\frac{5\pi}{40} < \frac{6\pi}{40}$$. Следовательно, $$\frac{\pi}{8} < \frac{3\pi}{20}$$. 5. Значит, $$tg(\frac{\pi}{8}) < tg(\frac{3\pi}{20})$$. Тогда $$-tg(\frac{\pi}{8}) > -tg(\frac{3\pi}{20})$$. 6. Таким образом, $$tg(-\frac{\pi}{8}) > tg(-\frac{3\pi}{20})$$. **Ответ: $$tg(-\frac{\pi}{8}) > tg(-\frac{3\pi}{20})$$** Предложенные варианты ответа не содержат верного.