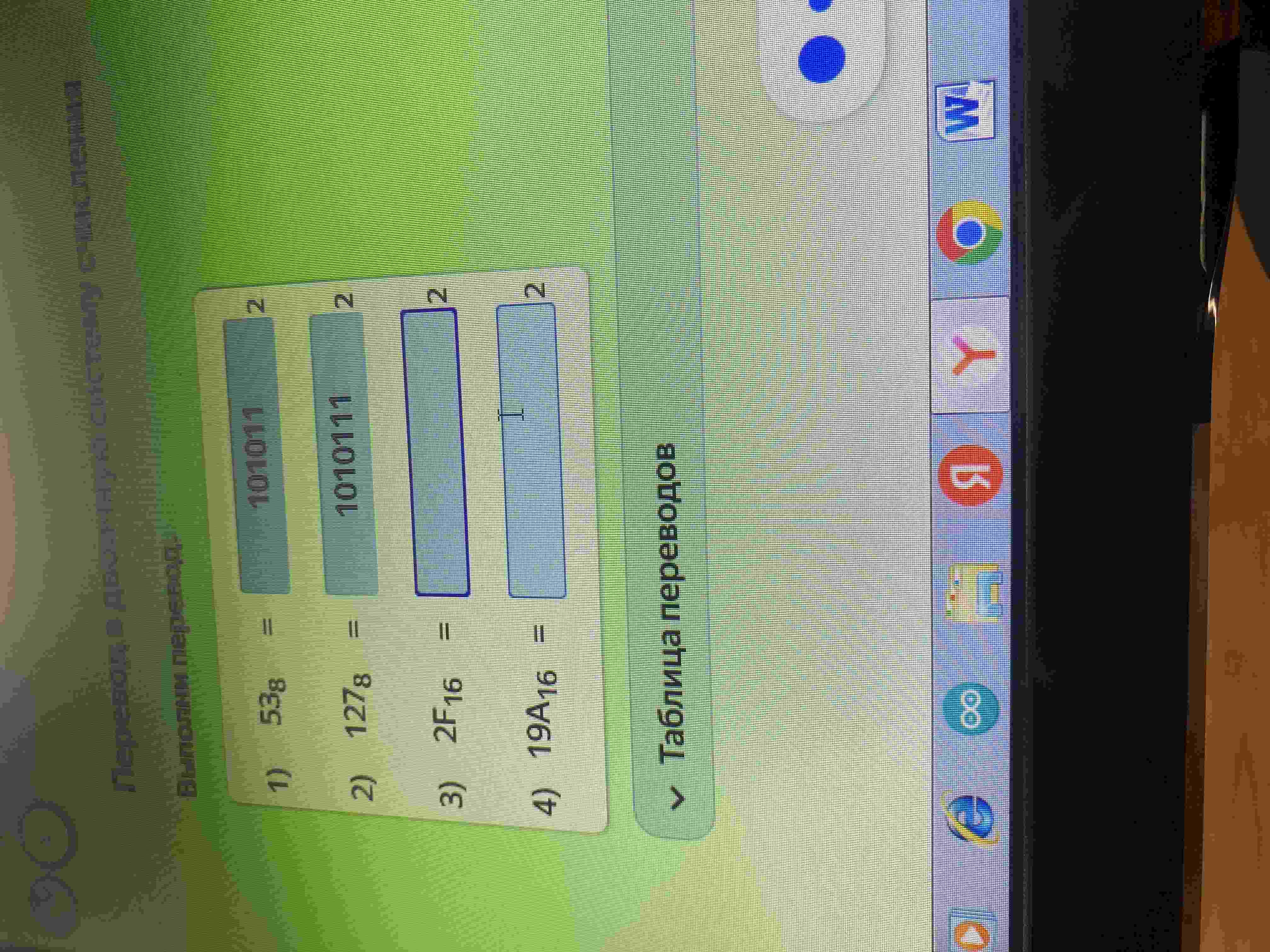
Выполни перевод из восьмеричной и шестнадцатеричной системы счисления в двоичную систему счисления: 1) 53_8 = ?_2 2) 127_8 = ?_2 3) 2F_{16} = ?_2 4) 19A_{16} = ?_2

Давай выполним перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления. 1) $53_8 = ?_2$ Восьмеричная система счисления использует цифры от 0 до 7. Каждая восьмеричная цифра может быть представлена тремя двоичными цифрами (битами). * 5 в двоичной системе: 101 * 3 в двоичной системе: 011 Объединяем эти двоичные представления: $53_8 = 101011_2$ Ответ: $101011_2$ 2) $127_8 = ?_2$ * 1 в двоичной системе: 001 * 2 в двоичной системе: 010 * 7 в двоичной системе: 111 Объединяем эти двоичные представления: $127_8 = 001010111_2$ Ответ: $001010111_2$ 3) $2F_{16} = ?_2$ Шестнадцатеричная система счисления использует цифры от 0 до 9 и буквы от A до F. Каждая шестнадцатеричная цифра может быть представлена четырьмя двоичными цифрами (битами). * 2 в двоичной системе: 0010 * F (15) в двоичной системе: 1111 Объединяем эти двоичные представления: $2F_{16} = 00101111_2$ Ответ: $00101111_2$ 4) $19A_{16} = ?_2$ * 1 в двоичной системе: 0001 * 9 в двоичной системе: 1001 * A (10) в двоичной системе: 1010 Объединяем эти двоичные представления: $19A_{16} = 000110011010_2$ Ответ: $000110011010_2$ Развёрнутый ответ для школьника: Мы перевели числа из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления. Важно помнить, что каждая цифра в восьмеричной системе представляется тремя двоичными цифрами, а каждая цифра в шестнадцатеричной системе представляется четырьмя двоичными цифрами. Затем мы просто объединили эти двоичные представления, чтобы получить окончательный результат.