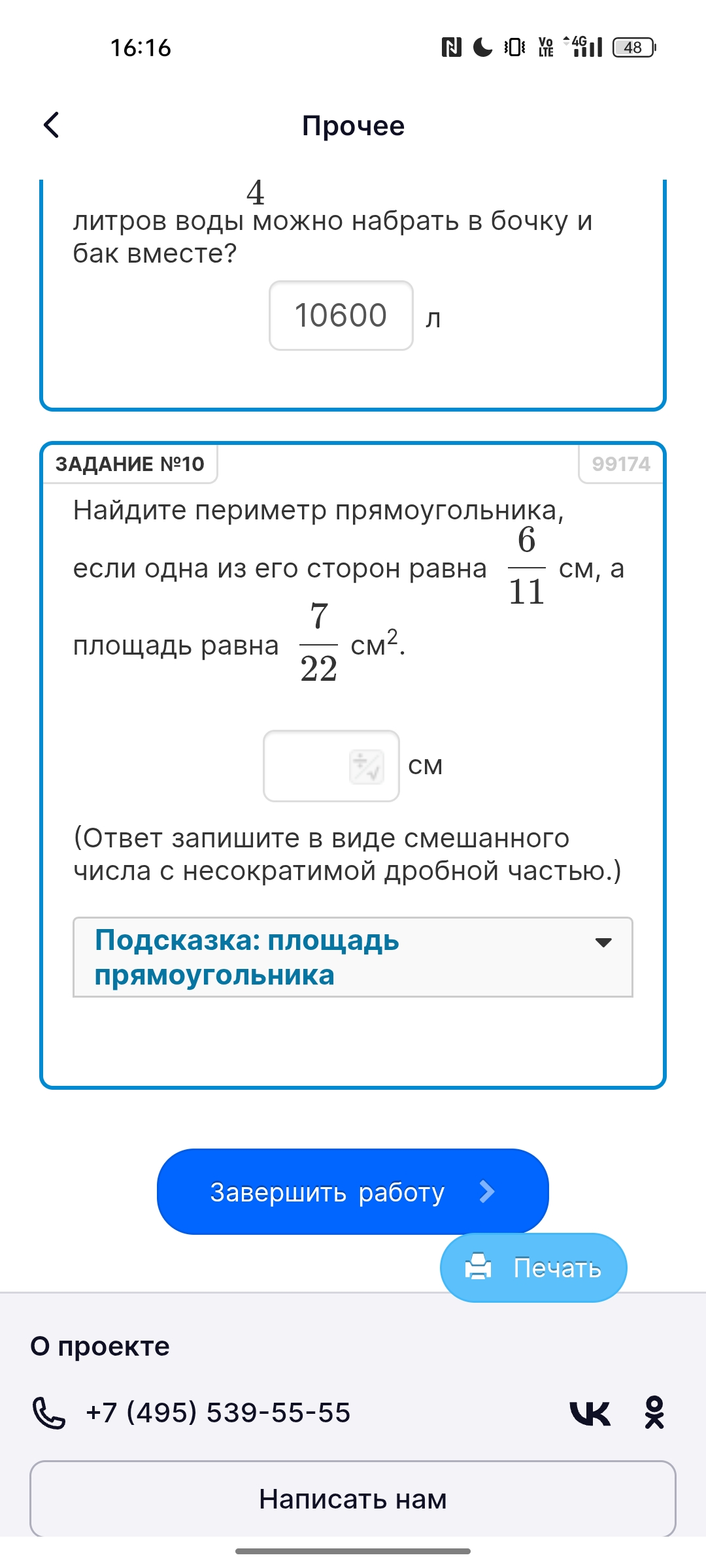
Задача 2: Найдите периметр прямоугольника, если одна из его сторон равна  6/11 см, а площадь равна 7/22 см².

Для решения этой задачи, нам нужно найти периметр прямоугольника, зная одну сторону и площадь. 1. **Определим формулу площади прямоугольника:** Площадь прямоугольника ( S = a cdot b ), где ( a ) - одна сторона, ( b ) - другая сторона. 2. **Найдем вторую сторону прямоугольника:** Нам известна площадь ( S = \frac{7}{22} ) и одна сторона ( a = \frac{6}{11} ). Подставим эти значения в формулу площади и найдем ( b ): \[\frac{7}{22} = \frac{6}{11} cdot b\] Чтобы найти ( b ), разделим площадь на известную сторону: \[b = \frac{\frac{7}{22}}{\frac{6}{11}} = \frac{7}{22} \cdot \frac{11}{6} = \frac{7 \cdot 11}{22 \cdot 6} = \frac{7 \cdot 1}{2 \cdot 6} = \frac{7}{12}\] Итак, вторая сторона прямоугольника ( b = \frac{7}{12} ) см. 3. **Определим формулу периметра прямоугольника:** Периметр прямоугольника ( P = 2(a + b) ), где ( a ) и ( b ) - стороны прямоугольника. 4. **Найдем периметр:** Подставим известные значения сторон ( a = \frac{6}{11} ) и ( b = \frac{7}{12} ) в формулу периметра: \[P = 2(\frac{6}{11} + \frac{7}{12})\] Чтобы сложить дроби, приведем их к общему знаменателю. Общий знаменатель для 11 и 12 равен 132. \[P = 2(\frac{6 \cdot 12}{11 \cdot 12} + \frac{7 \cdot 11}{12 \cdot 11}) = 2(\frac{72}{132} + \frac{77}{132}) = 2(\frac{72 + 77}{132}) = 2(\frac{149}{132})\] \[P = \frac{2 \cdot 149}{132} = \frac{298}{132}\] 5. **Упростим дробь:** Дробь \(\frac{298}{132}\) можно сократить, разделив числитель и знаменатель на 2: \[\frac{298}{132} = \frac{149}{66}\] 6. **Выразим в виде смешанного числа:** Разделим 149 на 66, чтобы получить смешанное число: \[149 \div 66 = 2 \text{ (остаток 17)}\] Таким образом, \(\frac{149}{66} = 2\frac{17}{66}\) **Ответ:** Периметр прямоугольника равен ( 2\frac{17}{66} ) см.