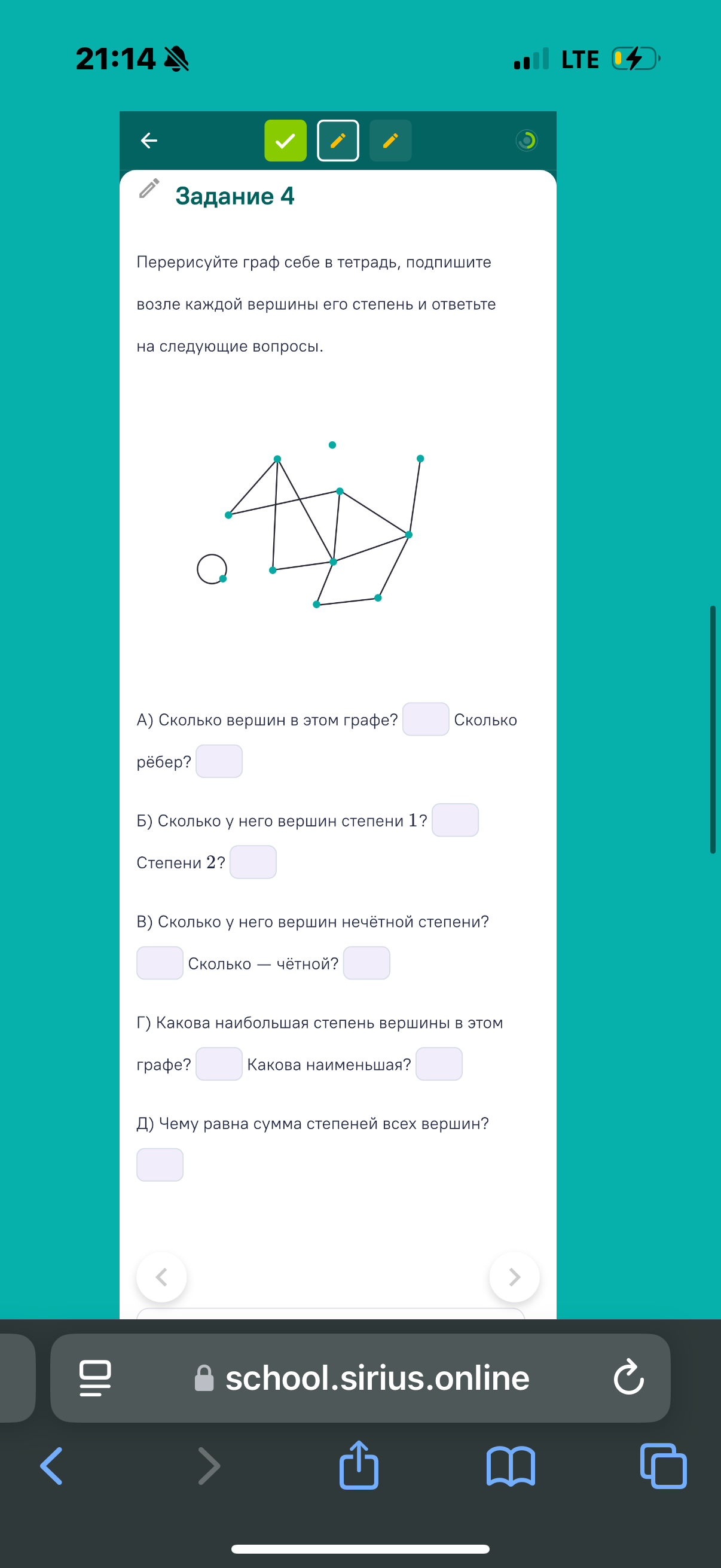
Задание 4. Перерисуйте граф себе в тетрадь, подпишите возле каждой вершины его степень и ответьте на следующие вопросы: А) Сколько вершин в этом графе? Сколько ребер? Б) Сколько у него вершин степени 1? Степени 2? В) Сколько у него вершин нечётной степени? Сколько – чётной? Г) Какова наибольшая степень вершины в этом графе? Какова наименьшая? Д) Чему равна сумма степеней всех вершин?

Чтобы ответить на вопросы, сначала определим степень каждой вершины графа. Степень вершины — это количество ребер, инцидентных этой вершине.

А) Считаем вершины и ребра:

• Вершины: На графе можно насчитать 8 вершин.
• Ребра: На графе можно насчитать 11 ребер.

Ответ: 8 вершин, 11 ребер

Б) Считаем вершины по степеням:

• Вершины степени 1: Одна вершина имеет степень 1. Это самая левая вершина на рисунке.
• Вершины степени 2: Три вершины имеют степень 2.

Ответ: 1 вершина степени 1, 3 вершины степени 2

В) Считаем вершины с четной и нечетной степенью:

• Нечетные вершины: 4 вершины имеют нечетную степень (1, 3, 3, 3).
• Четные вершины: 4 вершины имеют четную степень (2, 2, 2, 4).

Ответ: 4 вершины нечетной степени, 4 вершины четной степени

Г) Определяем наибольшую и наименьшую степень вершины:

• Наибольшая степень: Наибольшая степень вершины в графе равна 4.
• Наименьшая степень: Наименьшая степень вершины в графе равна 1.

Ответ: Наибольшая степень - 4, наименьшая степень - 1

Д) Считаем сумму степеней всех вершин:

Сумма степеней всех вершин графа равна удвоенному числу ребер. Так как ребер 11, то сумма степеней равна 2 * 11 = 22.

Ответ: 22