Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 778
Задание 778
\[\boxed{\text{778\ (778).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
Знаки сравнения:
\(> \ - \ \)больше
\(\mathbf{<} -\) меньше
Периметр треугольника – это сумма длин его трёх сторон:
\[\mathbf{P = a + b + c.}\]
Медиана треугольника – это отрезок в треугольнике, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине.
Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых.
Если почленно сложить верные неравенства одного знака, то получится верное неравенство.
Чтобы сложить почленно неравенства, нужно попарно сложить правые и левые части неравенства:
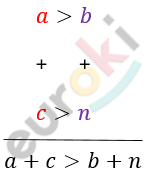
Решение.
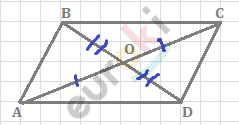
\[1)\ BO - медиана\ \]
\[треугольника\ \text{ABC}\ (m_{b})\]
\[BO = OD.\]
\[2)\ ABCD - параллелограмм,\ \]
\[(так\ как\ AO = OC).\]
\[3)\ Рассмотрим\ ⊿\ \text{ABD}:\]
\[по\ свойству\ сторон\ \]
\[⊿\ BC + AB > AC.\]
\[Сложим\ эти\ стороны:\]
\[+ \left| \begin{matrix} AB < BO + AO \\ BC < BO + OC \\ \end{matrix} \right.\ \]
\(\text{\ \ \ }\overline{AB + BC < BO + AO + BO + OC}\),
\[где\ AO + OC = AC \Longrightarrow\]
\[AB + BC < 2BO + AC\]
\[AB + BC - AC < 2BO\]
\[AB + BC - AC < 2mb\]
\[4)\ m_{a} = AO,\ \ m_{c} = CO\]
\[Рассмотрим\ ⊿\ ABD:\ \]
\[\ AB + AD > BD\]
\[+ \left| \begin{matrix} AB < BO + AO \\ AD < AO + OD \\ \end{matrix} \right.\ \]
\(\text{\ \ \ \ }\overline{AB + AD < BO + AO + AO + OD}\),
\[где\ BO + OD = BD \Longrightarrow\]
\[\Longrightarrow AB + AD < 2AO + BD\]
\[AB + AD - BD < 2AO\]
\[AB + AD - BD < 2ma\]
\[Рассмотрим\ ⊿\ BCD:\ \ \]
\[BC + CD > BD\]
\[+ \left| \begin{matrix} BC < BO + OC \\ CD < CO + OD \\ \end{matrix} \right.\ \]
\[\text{\ \ }\overline{BC + CD < BO + OC + OC + OD},\]
\[где\ BO + OD = BD \Longrightarrow\]
\[\Longrightarrow BC + CD < 2OC + BD\]
\[BC + CD - BD < 2OC\]
\[BC + CD - BD < 2mc\]
\[5)\ m_{a} + m_{b} + m_{c} = ?\]
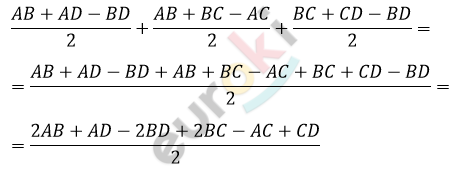
\[m_{a} > \frac{AB + AD - BD}{2},\ \ \]
\[m_{b} > \frac{AB + BC - AC}{2},\]
\[\text{\ \ }m_{c} > \frac{BC + CD - BD}{2}\]
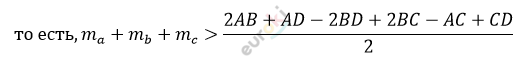
\[Таким\ образом,\ верхняя\ \]
\[и\ нижняя\ оценка\ суммы\ \]
\[медиан\ треугольника\]
\[определяется\ его\ периметром:\]
\[\frac{P}{2} < m_{a} + m_{b} + m_{c} < P.\]
\[\boxed{\text{778.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
| \[x^{2} + px + 405 = 0\] | \[\left( x_{2} - x_{1} \right)^{2} = 144\] |
|---|---|
| \[\left\{ \begin{matrix} x_{1} + x_{2} = - p \\ x_{1}x_{2} = 405\ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ }\] |
\[\left( x_{2} - x_{1} \right)^{2} = x_{2}^{2} - 2x_{1}x_{2} + x_{1}^{2} =\] \[= x_{1}^{2} + x_{2}^{2} - 2x_{1}x_{2} = x_{1}^{2} + x_{2}^{2} -\] \[- 2 \cdot 405 = 144\ \ \] |
\[x_{1}^{2} + x_{2}^{2} - 810 = 144\]
\[x_{1}^{2} + x_{2}^{2} = 954\]
\[x_{1}^{2} + x_{2}^{2} = x_{1}^{2} + 2x_{1}x_{2} + x_{2}^{2} -\]
\[- 2x_{1}x_{2} = \left( x_{1} + x_{2} \right)^{2} - 2x_{1}x_{2} =\]
\[= ( - p)^{2} - 2 \cdot 405 = 954\]
\[p^{2} - 810 = 954\]
\[p^{2} = 1764\]
\[p = \pm 42\]
\[Ответ:p = \pm 42\text{.\ \ }\]
